Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 159
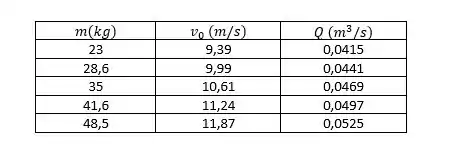
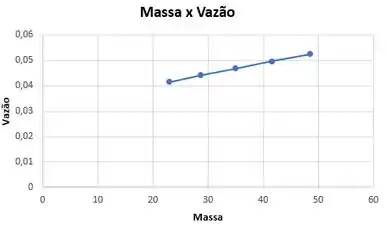
Um jato vertical de água sai de um bocal de de diâmetro. O jato atinge um disco horizontal (veja o Problema 4.158). O disco é restringido horizontalmente, mas está livre para se mover verticalmente. A massa do disco é . Trace um gráfico da massa do disco vazão para determinar a vazão de água requerida para elevar o disco acima do plano de saída do jato.
Passo 1
Considerações Iniciais:
- Escoamento em estado estacionário;
- Escoamento incompressível;
- Escoamento com velocidade constante (;
- Escoamento uniforme.
- Força de resistência desprezível;
- Não há presença de aceleração.
Passo 2
Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:
Como estamos analisando um sistema , temos:
Não a resistência nem aceleração, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Passo 3
Sendo , temos:
;
;
Temos então que a massa é dada por:
Passo 4
Temos o conhecimento apenas da velocidade e área da entrada, assim, utilizando a Equação de Bernoulli:
E sendo , temos que:
Passo 5
Agora, precisamos calcular , e por uma simples equação da continuidade conseguimos isso:
Passo 6
Substituindo a fórmula dos Passos 4 e 5 na equação da massa obtida no Passo 3, temos:
Agora, apenas substituiremos os dados na equação:
;
;
;
.
;
Então:
Sendo a vazão dada por:
Temos:
Precisamos de uma vazão de água de para elevar o disco acima do plano de saída do jato.
Passo 7
Gráfico da massa do disco vazão:
