Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 23

Quando levados a altas temperaturas, muitos combustíveis líquidos convencionais se dissociam em hidrogênio e outros componentes. Desta maneira, a vantagem de uma célula a combustível do tipo óxido sólido é que tal dispositivo pode, internamente, transformar facilmente combustíveis líquidos disponíveis em hidrogênio, que pode, então, ser usado para produzir potência elétrica de forma similar à do Exemplo 1.5. Considere uma célula a combustível portátil do tipo óxido sólido operando a uma temperatura Tcc = 800°C. A célula a combustível encontra-se no interior de um recipiente metálico cilíndrico de diâmetro D = 75 mm e comprimento L = 120 mm. A superfície externa do cilindro é isolada termicamente com um material de baixa condutividade térmica. Para uma aplicação específica, deseja-se que o registro térmico do recipiente seja pequeno, para evitar a sua detecção por sensores infravermelhos. O nível no qual o recipiente pode ser detectado por um sensor infravermelho pode ser estimado igualando-se o fluxo térmico radiante emitido pela superfície exterior do recipiente (Equação 1.5; Es = εsσTs^4) ao fluxo térmico emitido por uma superfície negra equivalente, (En = σTn^4). Se a temperatura da superfície negra equivalente, Tn, estiver próxima da temperatura da vizinhança, o registro térmico do recipiente é muito pequeno para ser detectado – não é possível distinguir o recipiente em relação à vizinhança.

(a) Determine a espessura de isolante necessária para ser aplicada sobre a parede cilíndrica do recipiente para garantir que o recipiente não se torne facilmente visível para um sensor de infravermelho (isto é, (Tn –Tviz)

(b) Calcule a temperatura da superfície externa do recipiente nos quatro casos (alta e baixa condutividade térmica; alta e baixa emissividade da superfície).

(c) Calcule a perda térmica pela parede cilíndrica do recipiente nos quatro casos.

Passo 1

Eu sei que o enunciado é muito grande, mas não fique com medo, se o Naruto não desistiu do sonho de se tornar Hokage não é o tamanho do enunciado da questão que deve te fazer desistir de resolvê-la.

Cola em mim que a gente vai resolver isso aí juntos!

Nessa questão, temos uma célula combustível cilíndrica operando a uma temperatura de , com a superfície externa do cilindro é isolada termicamente com um material de baixa condutividade térmica, como demonstra o esquema ilustrativo abaixo com algumas das propriedades que vamos utilizar:

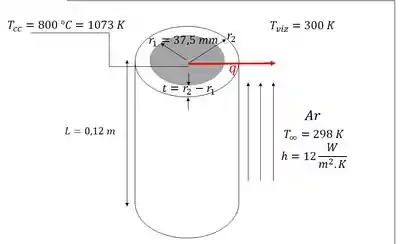
Além disso, temos que nos atentar a uma relação imposta pelo enunciado: como se deseja que o registro térmico do recipiente seja pequeno, para evitar a sua detecção por sensores infravermelhos, deve-se estipular o nível no qual o recipiente pode ser detectado por um sensor infravermelho pode ser estimado igualando-se o fluxo térmico radiante emitido pela superfície exterior do recipiente () ao fluxo térmico emitido por uma superfície negra equivalente, (). Sendo assim, a temperatura da superfície pode ser calculada com a seguinte expressão:

Sendo a emissividade da superfície do isolante.

Esse problema quer que a gente calcule o valor da espessura do isolante em quatro situações diferentes colocadas no enunciado, além de calcular a temperatura da superfície externa do isolante e, por fim, calcular a perda térmica (taxa de transferência de calor) pela parede cilíndrica do recipiente nos mesmo quatro casos.

Pra isso, a gente tem que montar o circuito térmico do nosso volume de controle, como demonstra o esquema ilustrativo abaixo:

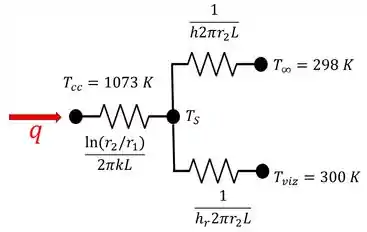
Dá pra perceber pela imagem que o circuito térmico pra nosso problema tem resistências a transferência de calor por radiação e por convecção em paralelo, amas em série a uma resistência à transferência de calor por condução.

Fazendo um balanço da taxa de transferência de calor por condução , chegamos a:

Onde essas taxas podem ser calculadas como:

, que é a taxa de transferência de calor do combustível até a superfície externa do isolante, sendo ;
, que é a taxa de transferência de calor por convecção a partir da parte externa do isolante;
, que é a taxa de transferência de calor por radiação a partir da parte externa do isolante, sendo , com .

Ou seja, nossa expressão pro balanço fica assim:

Caramba, foi muita informação! Mas agora nos próximos passos a gente vai resolver as letras (a), (b) e (c) do problema! Além disso, na resposta eu vou deixar uma tabela com todos os resultados que a gente calcular.

Passo 2

Primeiro, vamos resolver a letra (a) da questão.

Temos que calcular a espessura mínima para que a diferença máxima entre a temperatura de um corpo negro equivalente e a temperatura das vizinhanças seja de , de modo que para garantir que o recipiente não se torne facilmente visível para um sensor de infravermelho, ou seja, .

Dessa maneira, a temperatura da superfície é:

Agora, vamos montar quatro expressões (uma pra cada situação dada no enunciado do item (a)) e calcular o valor da espessura do isolante:

Para e

Agora devemos resolver essa equação. Aqui utilizamos solver do programa Scilab, mas você pode utilizar o solver do Excel (ou outros programas) ou até mesmo o método de busca direta na sua calculadora.

Sendo assim: