Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 13
Uma placa de alumínio quadrada, com de espessura e de lado, é aquecida enquanto permanece suspensa, em posição vertical, em ar quiescente a . Determine o coeficiente de transferência de calor médio na placa quando sua temperatura é de , através de dois métodos: usando resultados da solução por similaridade das equações da camada limite e usando resultados obtidos com uma correlação empírica.
Passo 1
Ora ora, o que nós temos aqui? Nessa questão nos foi dado uma placa de alumínio quadrada a suspensa em ar inativo a . Esquematicamente:
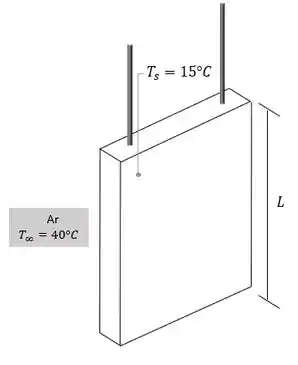
Com isso, precisamos encontrar o coeficiente médio de transferência de calor por dois métodos: usando resultados de similaridade da camada limite e resultados de uma correlação empírica, beleza?
Passo 2
Para resolver essa questão vamos assumir:
(1) Temperatura uniforme da superfície da placa;
(2) Ar ambiente quieto;
(3) Troca de radiação da superfície com ambientes é desprezível;
(4) Comportamento perfeito do gás para o ar, .
Além disso, as propriedades do ar vão ser retiradas da Tabela A.4 onde,
Calcule o número de Rayleigh para determinar as condições de fluxo da camada limite,
Substituindo os valores temos,
Onde e
Passo 3
Como , o fluxo é laminar e a solução de similaridade da Seção 9.4 é aplicável.
Onde,
Substituindo os valores numéricos com , temos:
Passo 4
A correlação empírica apropriada para estimar é:
Substituindo os valores,
Resposta
e