Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 3.Problemas - Ex. 14

Seja a parede composta do Problema 3.13 sob condições para as quais o ar interior ainda é caracterizado por T ∞ , i = 20 ° C   e   h i = 30   W / ( m 2 ⋅   K ) . Entretanto, use condições mais realistas para o ar externo, caracterizando-o por uma variação diurna (tempo) da temperatura na forma

T ∞ , e K = 273 + 5 sin ⁡ 2 π 24 t                         0 ≤ t ≤ 12 h

T ∞ , e K = 273 + 11 sin ⁡ 2 π 24 t                               12 ≤ r ≤ 24   h

com h e = 60   W / ( m 2 ⋅ K ) . Supondo condições pseudo-estacionárias, nas quais mudanças na quantidade de energia armazenada no interior da parede podem ser desprezadas, estime a perda diária de calor através da parede se a sua área superficial total for igual a 200   m 2   .

Passo 1

E ai seres de luz, tudo bem?

Como diz o Homer “Filho, este aparelhinho vai nos ajudar a escapar dessa fria!”

  1. A temperatura do ar interno é de T ∞ , i   = 293   K
  2. Os coeficientes convectivos são h i = 30   W / m 2 ⋅ K e h o = 60   W / m 2 ⋅ K
  3. As temperaturas do ar externo são dadas por

    4. T ∞ , e K = 273 + 5 sin ⁡ 2 π 24 t                         0 ≤ t ≤ 12 h

    T ∞ , e K = 273 + 11 sin ⁡ 2 π 24 t                               12 ≤ r ≤ 24   h

  4. A área total da superfície da parede é A = 200   m 2
  5. Dado L p = 0.01   m ; L b = 0.1   m ; L s = 0.020   m

O exercício quer que nós determinemos a perda diária de calor através da parede, Q = ?

O circuito equivalente é o seguir:

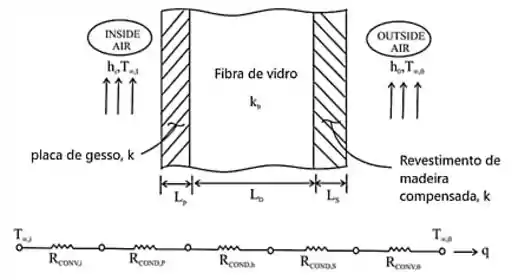
Passo 2

A perda de calor da parede é obtida partindo da equação de taxa, bem como

Q = ∫ 0 24 h T ∞ , i   - T ∞ , o d t R t o t

Partindo das condições que foram prescritas

∫ 0 24 h T ∞ , i   - T ∞ , o d t = ∫ 0 12 h T ∞ , i   - T ∞ , o d t + ∫ 12 h 24 h T ∞ , i   - T ∞ , o d t

Ou

∫ 0 24 h T ∞ , i   - T ∞ , o d t = ∫ 0 12 h 293 - 273 - 5 sin ⁡ 2 π 24 t d t + ∫ 12 h 24 h 293 - 273 - 11 sin ⁡ 2 π 24 t d t

Passo 3

Calculando as integrais

∫ 0 24 h T ∞ , i   - T ∞ , o d t = 20 t + 5 24 2 π cos ⁡ 2 π 24 t 0 12 h + 20 t + 11 24 2 π cos ⁡ 2 π 24 t 12 h 24 h

Aplicando os limites, temos

∫ 0 24 h T ∞ , i   - T ∞ , o d t = 20 × 12 h K + 120 2 π - 1 - 1 h K + 20 × 24 - 12 h K + 264 2 π 1 + 1 h K

∫ 0 24 h T ∞ , i   - T ∞ , o d t = 480 h K + 45.83 h K = 480 + 45.83 × 3600   K s

∫ 0 24 h T ∞ , i   - T ∞ , o d t = 1892988   K s

Passo 4

Partindo das condições que foram prescritas, a resistência térmica total é expressa como

R t o t = R c o n v , i + R c o n d , p + R c o n d , b + R c o n d , s + R c o n v , o

= 1 h i A + L p k p A + L b k b A + L s k s A + 1 h o A

R t o t = 1 A 1 h i + L p k p + L b k b + L s k s + 1 h o

Para T = 300   K

A manta de fibra de vidro, k b = 0.038   W / m ⋅ K

Revestimento de madeira compensada, k s = 0.12   W / m ⋅ K

Placa de gesso, k p = 0.17   W / m ⋅ K

R t o t = 1 A 1 h i + L p k p + L b k b + L s k s + 1 h o

= 1 200 1 30 + 0.01 0.17 + 0.1 0.038 + 0.02 0.12 + 1 6 0

= 0.0 14535   K / W

Passo 5

Agora vamos finalizar ela substituindo alguns valores que temos para encontrarmos a perda de calor através da parede

q = 1892988 0.014535

q = 130236.532   k J

Portanto, a perda de calor através da parede é de 130.236   M J .

“Eu não estava mentindo! Estava escrevendo ficção com a boca.”

Resposta

Portanto, a perda de calor através da parede é de 130.236   M J .

Exercícios de Livros Relacionados

Uma parede composta separa gases de combustão a 2400 ° C de um líquido refrigerante a 100 ° C , com coeficientes de transferência de calor no lado do gás e no do líquido iguais a 25 e 1000W / ( m 2 ·
Considere uma parede plana composta constituída por dois materiais com condutividades térmicas k A = 0,09W / ( m · K ) e k B = 0,03W / ( m · K ) e espessuras L A = 8m m e L B = 16m m . A resistência d
Considere um transistor de potência encapsulado em uma caixa de alumínio que é fixado em sua base a uma placa quadrada de alumínio de condutividade térmica k = 240W / m ⋅ K , espessura L = 8m m e larg
Um longo fio de Constantan de 1m m de diâmetro é soldado a topo à superfície de um grande bloco de cobre, formando uma junção de termopar. O fio se comporta como uma aleta, permitindo que o calor flua
Um dissipador de calor de alumínio ( k = 230W / m ⋅ K ), usado para resfriar uma matriz de chips eletrônicos, consiste em um canal quadrado de largura interna w = 30m m , através do qual o fluxo de lí