Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 47
Quando lidamos com a lubrificação de rolamentos, a equação de governo que descreve a pressão é a equação de Reynolds, geralmente descrita em uma dimensão como:
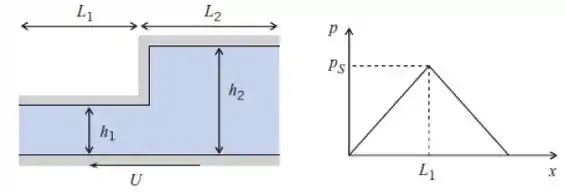
Em que é a altura do degrau e é a velocidade da superfície inferior. O degrau tem um desenho relativamente simples, no qual são usados fluidos de baixa viscosidade, como água, gasolina e solventes. A espessura mínima do filme nessas aplicações é muito pequena. A altura do degrau deve ser pequena o suficiente para ter boa capacidade de carga, mas grande o suficiente para não ficar, depois de algum desgaste, liso e plano. Usando a equação unidirecional para o movimento do fluido na direção , mostre que a distribuição de pressão no degrau do rolamento é a mostrada no gráfico, em que:
Passo 1
Tá legal, a primeira coisa que devemos fazer é escrever as equações de Navier-Stokes, então, teremos:
Essa será nossa equação 1. Ainda temos:
Essas serão nossas equações 2, 3 e 4 respectivamente. Beleza! Agora vem a parte das considerações, sabemos que nesse caso temos regime permanente, então podemos cancelar os termos dependentes do tempo das equações 2, 3 e 4. Temos também que o escoamento é incompressível, então . Agora, sabemos que não teremos nenhuma variação ou alteração na direção , de modo que o restante da sua equação 4, além do termo no tempo que já cancelamos, será zero. E também todos os outros termos nas equações 1, 2 e 3 que dependem de serão iguais a zero.
Agora, assumindo escoamento totalmente desenvolvido, não teremos nenhuma variação de propriedade na direção , com exceção da pressão, então todas as derivadas com relação a podem ser igualadas a zero. Podemos também desconsiderar as forças de campo na direção e , de modo que . Então, até o momento, as equações se tornaram:
Passo 2
Agora, da primeira equação vimos que a derivada da velocidade em é igual a zero, desse modo, como é zero na superfície sólida, então, já que deve ser constante, ele é zero para todo o intervalo, desse modo, podemos zerar os termos que apresentam nas outras duas equações, e elas se tornam:
Com isso, a pressão não depende de , ela pode depender, no máximo, de . Então, analisando a equação restante na direção , temos:
Dessa última equação, podemos notar que temos um termo que depende de e outro que depende de e os dois somando devem se anular, dessa forma, isso só será satisfeito em todos os casos se os dois termos forem constantes, dessa forma, teremos então:
E, isso implica em:
Então agora vamos resolver a equação diferencial integrando ela duas vezes em , desse modo, temos:
Integrando novamente em , temos:
Passo 3
Agora precisamos resolver essa equação com as condições de contorno conhecidas, precisamos resolvê-la separadamente, uma vez para a primeira região e depois para a segunda região. Então, começando pela primeira região, com o auxílio do diagrama do enunciado, temos as seguintes condições de contorno:
Então, aplicando a primeira condição de contorno, temos:
E, da segunda condição, temos:
Então, a equação para a primeira parte do trecho será:
Substituindo o termo do gradiente de pressão, chegamos em:
Passo 4
Agora vamos repetir o processo feito no passo 3, só que para a segunda região, onde temos as seguintes condições de contorno:
Então, aplicando a primeira condição de contorno, temos:
E, da segunda condição, temos:
Então, a equação para a primeira parte do trecho será:
Substituindo o termo do gradiente de pressão, temos:
Passo 5
Agora, para relacionar as duas velocidades, vamos utilizar o princípio da continuidade, já que sabemos que a vazão deve ser a mesma nos dois pontos, então temos:
Substituindo as expressões encontradas para a velocidade nos passos 3 e 4, temos:
Vamos resolver uma integral de cada vez, dessa forma, começando pela integral da esquerda, temos:
Substituindo os limites de integração, temos:
Agora, resolvendo a integral do lado direito lá em cima, temos:
Substituindo os limites de integração, temos:
Passo 6
E, agora, igualando as duas expressões encontradas, temos:
Agora, colocando o termo em evidência, temos:
E, finalmente, chegamos na equação dada no enunciado, então, teremos:
Resposta
Ei, a resposta está no passo a passo :)