Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 94
Reconsidere o Problema 8-93. Fazendo a queda de pressão variar entre 1 kPa e 10 kPa, calcule a vazão a intervalos de 1 kPa, e mostre-a graficamente versus a queda de pressão
Passo 1
Faaaaala galerinha, animados?
Esta aqui é bem maneira !!
Do problema anterior nós vimos que:
E a razão entre os diâmetros:
Agora o único dado que precisamos é da área do orifício:
Substituindo para achar a queda de pressão:
Então já achamos uma função da vazão versus a queda, só o que precisamos é substituir:
Agora faremos o gráfico:
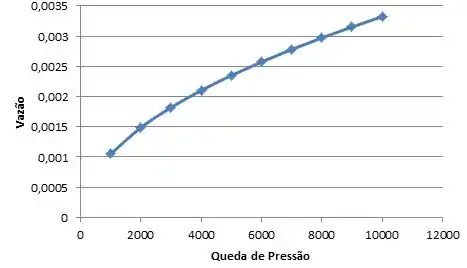
E chegamos ao fim de mais umaa !!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Quando lidamos com a lubrificação de rolamentos, a equação de governo que descreve a pressão é a equação de Reynolds, geralmente descrita em uma dimensão como: d d x h 3 μ . d p d x + 6 U . d h d x =
A força de fixação de uma peça durante uma operação de torneamento mecânico é causada por óleo de alta pressão suprido por uma bomba. O óleo vaza axialmente através de um espaço anular com diâmetro D
8.73 Laufer mediu os seguintes dados para velocidade média no escoamento turbulento completamente desenvolvido em tubos, para R e U = 50000 :Além disso, Laufer mediu os seguintes dados para velocidade
Considere, primeiro, água e, em seguida, óleo lubrificante S A E10 W fluindo a 40 ° C em um tubo de 6m m de diâmetro. Determine, para cada fluido, a máxima vazão (e o correspondente gradiente de press
Para escoamento laminar completamente desenvolvido em um tubo, determine a distância radial a partir do eixo do tubo na qual a velocidade iguala-se à velocidade média.