Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 119

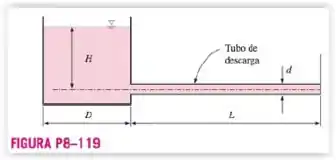
Um líquido altamente viscoso é descarregado de um grande contêiner através de um tubo com diâmetro pequeno em escoamento laminar. Desprezando os efeitos da entrada e as cargas de velocidade, obtenha uma relação para a variação da profundidade do fluido no tanque com o tempo.

Passo 1

Bom, nesse problema nós temos que obter uma relação que caracterize a variação da profundidade do fluido no tanque com o tempo.

Primeiramente, vamos estabelecer os pontos para utilizarmos a equação de energia:

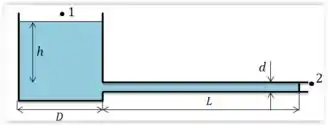
Pelo diagrama, nós temos que os pontos 1 e 2 entram em contato com a atmosfera logo, P 1 = P 2 = P a t m . Além, disso, a velocidade no ponto 1 é aproximadamente V 1 ≅ 0 , enquanto V 2 é desprezível. A altura no ponto 1 é z 1 = h e no ponto 2 é de referência, ou seja, z 2 = 0 . O efeito das entradas é desprezível, α = 1 . Por ultimo, não temos bomba nem turbina, então h b o m b a = 0 e h t u r b i n a = 0 . Logo:

P 1 ρ g + α 1 V 1 2 2 g + z 1 + h b o m b a = P 2 ρ g + α 2 V 2 2 2 g + z 2 + h t u r b i n a + h L

z 1 = h L       ∴           h = h L

Passo 2

Como o escoamento é totalmente desenvolvido, ele é laminar, ou seja, o fator de atrito é dado por f = 64 R e . Vamos calcular a perda de carga:

h L = f L D V 2 2 g

h L = 64 R e L d V 2 2 g

O fluido tem alta viscosidade então nós podemos buscar uma relação com isso pelo numero de Reynolds:

h L = 64 V d v L d V 2 2 g                     ∴                     h L = 64 v V d L d V 2 2 g                   ∴                         h L = 64 v L d 2 V 2 g

Outra transformação que podemos fazer é aplicando a vazão pela velocidade:

h L = 64 v L d 2 v ˙ A 2 g                   ∴                     h L = 64 v L d 2 1 2 g 4 v ˙ π d 2                 ∴             h L = 128 v L π d 4 v ˙ g  

Passo 3

Agora, iremos aplicar a derivada como forma de expressar a altura diminuindo com o fluxo e isso leva em conta o tempo:

v ˙ = - A d h d t               ∴           v ˙ = - π D 2 4 d h d t

Substituimos essa expressão na ultima do Passo 2 :

h L = 128 v L π d 2 1 g - π D 2 4 d h d t

h L = - 32 v L D 2 d 2 g d h d t

Agora isolamos o d t :

d t = - 32 v L D 2 d 2 g d h h

Aplicamos a integração no intervalo de t < t < 0 e H < h < h :

∫ 0 t d t = - 32 v L D 2 d 2 g ∫ H h d h h

t = - 32 v L D 2 d 2 g [ ln ⁡ h - ln ⁡ H ]

Trocando os sinais:

t = 32 v L D 2 d 2 g [ ln ⁡ H - ln ⁡ h ]

t = 32 v L D 2 d 2 g [ ln ⁡ H h ]

Prontinho!!

Resposta

t = 32 v L D 2 d 2 g [ ln ⁡ H h ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura P6.101 mostra um ensaio de perdas para um filtro espesso. A vazão no tubo é de 7 m³/min e a pressão a montante é de 120 kPa. O fluido é o ar a 20 ° C. Usando a leitura do manômetro de coluna
Uma grande sala usa um ventilador para succionar o ar atmosférico a 20 ° C por um duto de aço comercial de 30 cm por 30 cm e 12 m de comprimento, como na Figura P6.92. Calcule (a) a vazão de ar em m³/
Um tubo de aço comercial de 12,2 m de comprimento e seção anular com a = 25 mm e b = 13 mm conecta dois reservatórios cuja diferença entre os níveis das superfícies é de 6,1 m. Calcule a vazão em L/s
Água a 20 ° C escoa por um duto liso de seção quadrada de 20 cm de lado a um número de Reynolds de 100.000 (regime turbulento). Para uma medição por meio de um “elemento de escoamento laminar”, deseja
Reconsidere a mesa de hóquei de ar do Problema 3.162, mas incluindo as perdas localizadas. A mesa tem área de 0,9 X 1,8 m, com furos de 1,6 mm de diâmetro, espaçados de 25 mm, formando uma malha retan