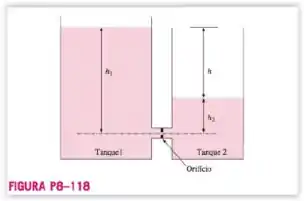
Um sistema que consiste em dois tanques cilíndricos interconectados com e deve ser usado para determinar o coeficiente de descarga de um orifício curto com diâmetro . No início , as alturas do fluído nos tanques são e , como mostra a Figura . Se são precisos para que os níveis do fluído dos dois tanques se igualem e o escoamento pare, determine o coeficiente de descarga do orifício. Despreze todas as outras perdas associadas a esse escoamento.
Passo 1
Bom, nesse problema precisamos determinar o coeficiente de descarga do orifício, que consiste basicamente num fator de correção de perdas.
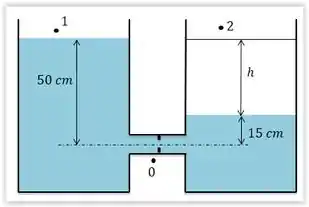
Como podemos desprezar as perdas associadas ao escoamento, podemos aplicar a equação de Bernoulli. Assim, criamos o diagrama estabelecendo pontos:
Passo 2
Pelo diagrama, nós temos um ponto que entra em contato com a atmosfera logo, ; e o ponto no orifício com a pressão total do sistema, logo, . Além, disso, a velocidade no ponto é aproximadamente , uma vez que é baixa. Por fim, a altura no ponto é de referência, ou seja, .
A partir da nossa analise, podemos substituir na equação:
Isolamos a velocidade:
Que, ao final, deve ser:
Passo 3
Pela definição de coeficiente de descarga, temos:
Podemos encontrar uma relação entre a altura e o tempo, sabendo que a massa se conserva. A distância vertical entre os níveis de agua é dado por , imaginamos que a tendência é diminuir durante a descarga enquanto e aumentam.
Assim, relacionando as seções com a altura, temos:
Estabelecendo uma variação para a distância vertical, temos:
Isolando que achamos nas relações com a altura e substituindo na expressão acima, obtemos:
Passo 4
Agora podemos relacionar com o coeficiente de descarga através do orifício:
Substituindo..
Organizamos os termos, tempo para o lado e altura para outro:
Aplicamos a integração com intervalos de e :
Por fim, isolamos :
Passo 5
Substituindo os dados:
Prontinho!!