Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 70

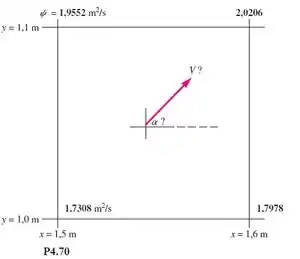
Um modelo CFD do escoamento incompressível permanente bidimensional imprimiu os valores da função corrente ψ (x, y), em m²/s, em cada um dos quatro cantos de uma pequena célula de 10 cm por 10 cm, como mostra a Figura P4.70. Use esses números para calcular

a velocidade resultante no centro da célula e seu ângulo a com relação ao eixo x.

Passo 1

Bora pra mais uma!

Antes de tudo vamos fazer uma breve analise do experimento. Os valores da função corrente são maiores na parte superior do que na parte inferior, o que indica que o sentido de u é para a direita. Da mesma forma, os valores são maiores à esquerda, o que indica que o sentido de v   é para baixo.

Agora, para estimar a velocidade resultante no centro da célula vamos calcular os valores médios de ψ nas laterais:

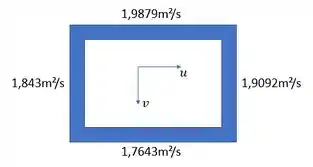
Então, no centro da célula:

u c e n t r o = ∆ ψ ∆ y = 1,9879 m 2 s - 1,7643 m 2 s 1,1 m - 1,0 m = 2,236 m s  

v c e n t r o = ∆ ψ ∆ x = 1,9092 m 2 s - 1,843 m 2 s 1,6 m - 1,5 m = 0,662 m s .

Então a velocidade no centro da célula é dada pelo modulo deste vetor, dada por:

V = 2,236 m s 2 + ( 0,662 m s ) ² = 2,332 m s .  

Passo 2

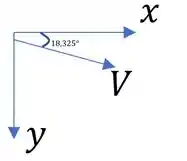
Agora, vamos calcular o ângulo resultante em relação ao eixo x.

α = arctan ⁡ 0,662 m s 2,236 m s = 18 , , 325 °   .

Resposta

A velocidade resultante no centro da célula tem valor de 2,332 m s e forma um ângulo de   18 , , 325 ° com o eixo X, conforme abaixo explicitado:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.28 A função de corrente para certo ampo de escoamento incompressível é dada pela expressão ψ = - U rs e nθ + q θ / 2 π . Obtenha uma expressão para o campo de velocidade. Encontre o(s) ponto(s) de e
5.25 Exemplo 5.7 é V → = U ( y / h ) î î. Dermine a função de corrente para este escoamento. Localize a linha de corrente que divide a vazão volumétrica total em duas partes iguais.
5.33 Deduza a função de corrente que representa a aproximação senoidal usada para modelar a componente x da velocidade na camada limite do Problemas 5.12. Localize as linhas de corrente a um quarto e
A large Rankine oval, with a 5 1 m and h 5 1 m, isimmersed in 208C water fl owing at 10 m/s. The upstreampressure on the oval centerline is 200 kPa. Calculate (a) thevalue of m; and (b) the pressure o
Water at 208C fl ows past a 1-m-diameter circular cylinder.The upstream centerline pressure is 128,500 Pa. If the lowest pressure on the cylinder surface is exactly the vaporpressure, estimate, by pot