Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 69
Um escoamento permanente, bidimensional, tem o seguinte potencial de velocidade em coordenadas polares:
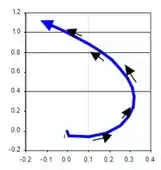
em que C e K são constantes. Determine a função corrente para esse escoamento. Para um crédito extra, seja C uma escala da velocidade U e K = UL, faça um esboço do que o escoamento pode representar.
Passo 1
Bora pra mais uma!
Vamos definir a função corrente, sabemos que:
Integrando ambas as equações:
Daí, obtemos a função corrente:
Sendo c uma constante.
Resposta
A função corrente é:
Sendo c uma constante. O escoamento é representado no esboço abaixo:
Exercícios de Livros Relacionados
A 22-cm-diameter solid aluminum sphere (SG 5 2.7) is accelerating at 12 m/s2 in water at 208C. (a) According to potential theory, what is the hydrodynamic mass of the sphere?(b) Estimate the force bei
For the velocity distribution u 5 2By, υ 5 1Bx, w 5 0,evaluate the circulation Γ about the rectangular closedcurve defined by (x, y) 5 (1,1), (3,1), (3,2), and (1,2). Interpret your result, especially
Assume that the Flettner rotor ship of Fig. P8.54 has a water resistance coeffi cient of 0.005. How fast will the shipsail in seawater at 208C in a 20-ft/s wind if the keel alignsitself with the resul
An incompressible plane flow has the velocity potentialϕ 5 2Kxy, where B is a constant. Find the stream functionof this fl ow, sketch a few streamlines, and interpret the flowpattern
The vertical keel of a sailboat approximates a Rankine oval125 cm long and 30 cm thick. The boat sails in seawater instandard atmosphere at 14 knots, parallel to the keel. At asection 2 m below the su