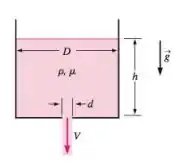
O líquido escoa por um orifício na parte inferior de um tanque como mostra a figura abaixo. Considere o caso no qual o orifício é muito pequeno comparado ao tanque . As experiências revelam que a velocidade média do jato é quase independente de . Na verdade, para uma ampla variedade desses parâmetros, só depende da altura da superfície líquida e da aceleração gravitacional . Se a altura da superfície líquida dobrar, com todas as outras condições iguais, por qual fator a velocidade média do jato aumentará?

Como primeira hipótese, o número de dimensões primárias representadas no problema e. Logo, para a redução, temos:

Com isso, temos:

Logo, temos apenas um permanece e, portanto, é definido como uma constante. O resultado final da análise dimensional é dado por:

Assim, quando é dobrado, podemos calcular facilmente o fator pelo qual aumenta, temos:

Logo, podemos concluir que quando dobramos , temos um aumento de de fator .