Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 120
Uma barra uniforme de madeira (d = 0,65) tem 10 cm por 10 cm por 3 m e está articulada em A, como mostra a Figura P2.120. A que ângulo theta a barra flutuará em água a 20°C?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.8 do livro, chamada “Empuxo; princípios de Arquimedes”.
Nesse problema, como mostra a figura que ilustra a questão, temos uma barra de madeira de de comprimento e de base . A parra faz um ângulo desconhecido com a horizontal.
Além disso, sabemos que esta barra está fixa em um ponto articulado , localizado a da superfície livre de água.
O enunciado pede que a gente calcule o ângulo para fazer com que a barra flutue.
Pra resolvê-la, a gente tem que analisar quais forças estão agindo nessa situação. Vamo ver a figura abaixo:
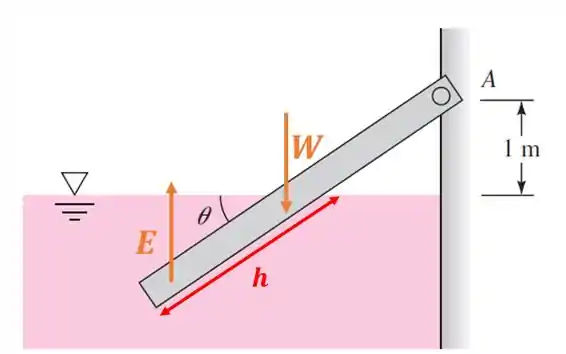
Sendo: o empuxo; o peso da haste de madeira de densidade .
Note que a gente não tem o valor do comprimento da haste submerso . Nos próximos passos, vamos descobrir esse valor fazendo um balanço de momento com relação ao ponto e com vamos calcular o ângulo
Vem comigo pra resolver a questão!
Passo 2
Nesse passo, vamos calcular as forças de empuxo e peso atuando na barra de madeira.
A primeira delas é o empuxo . O empuxo pode ser calculado a partir do produto do peso específico da água e do volume da barra submerso.
Pra entender essa parte, vamo ver o esquema lá em cima. Temos um comprimento da parte submersa da barra. Então, o volume submerso da barra será calculado utilizando o comprimento desconhecido e deixaremos o valor de em função dele.
Sendo assim:
O peso da madeira pode ser calculada a partir da equação:
Passo 3
Agora, vamos encontrar as linhas de ação do empuxo e do peso com relação ao ponto .
Vamos olhar neste outro esquema:
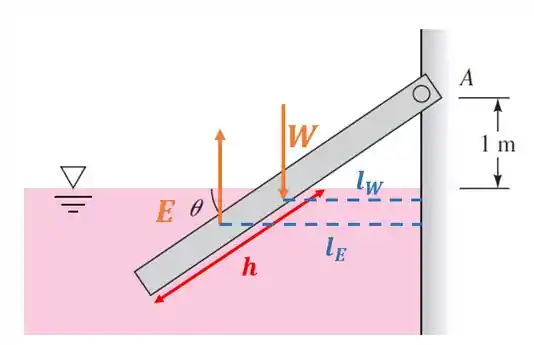
O enunciado diz que a barra é uniforme. Isso quer dizer que podemos dizer que a força peso está aplicada toda no centro da barra e o empuxo está aplicado no centro da parte submersa da barra.
Por isso, olhe a linha de ação da força peso com relação ao ponto , que chamamos de Como você pode notar, temos a formação de um triângulo retângulo de hipotenusa e cateto adjacente .
Usando uma simples relação trigonométrica, temos:
Por outro lado, como o empuxo está aplicada no meio da parte submersa, o triângulo retângulo formado tem hipotenusa de valor e cateto oposto . Sendo assim:
Com e podemos fazer o balanço de momento.
Passo 4
Pra finalizar a questão, vamo fazer o balanço de momento de e com relação ao ponto . Como queremos que a barra flutue, o balanço de momento deve ser igual a zero:
Resolvendo essa equação de segundo grau, obtemos os seguintes valores pra h:
Como é um valor maior que a própria barra, sabemos que este não é o valor correto.
Para calcular o ângulo , basta que a gente volte na figura esquemática. Temos um triângulo de hipotenusa (a parte emersa da barra) e cateto oposto (a distância do ponto A até a água). Sendo assim, usamos a seguinte relação para calcular o ângulo :
Pronto, matamos a questão juntos!
Resposta
O ângulo para o qual a barra flutuará em água é