Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 63

Um longo bastão de pirocerâmica com 20 mm de diâmetro é revestido por um tubo metálico muito fino para proteção mecânica. A fixação entre o bastão e o tubo tem uma resistência térmica de contato de R’t,c = 0,12 m · K/W.

(a) Se o bastão está inicialmente a uma temperatura uniforme de 900 K e é subitamente resfriado pela sua exposição a uma corrente de ar, na qual T∞ = 300 K e h = 100 W/(m2 · K), em qual instante de tempo a temperatura no eixo central do bastão atinge 600 K?

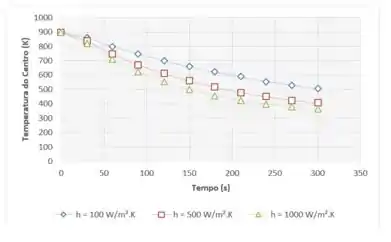
(b) O resfriamento pode ser acelerado pelo aumento da velocidade do ar e, portanto, do coeficiente convectivo. Para valores de h = 100, 500 e 1000 W/(m2 · K), calcule e represente graficamente as temperaturas no eixo central e na superfície do bastão de pirocerâmica em função do tempo para 0 ≤ t ≤ 300 s. Comente a respeito das implicações de melhorar o resfriamento do bastão exclusivamente pelo aumento no valor de h.

Passo 1

Vamos analisar o enunciado juntos e entender o que o problema quer de você.

Temos um bastão cilíndrico de 20 mm de diâmetro, revestido por um tubo metálico muito fino, que é resfriado por uma corrente de ar.

Em primeiro lugar, devemos calcular o tempo necessário para a temperatura da superfície atingir T 0 = 600   K   .

Por isso, se a gente supor tempos muito longos ( F o > 0,2 ) podemos modelar a temperatura adimensional no plano central ( r * = 0 ) a partir da equação:

ϴ 0 * = T 0 - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o )

Sendo   C 1 e ζ 1 coeficientes que podem ser calculados a partir da Tabela 5.1, F o o adimensional Número de Fourier, T 0 a temperatura no centro depois do tempo decorrido, T i a temperatura inicial e T ∞ a temperatura do ar.

Em um segundo momento, iremos representar graficamente a evolução da temperatura para o eixo central do cilindro e para sua superfície, considerando diferentes valores de coeficiente de convecção h .

Para isso, se a gente supor novamente tempos muito longos ( F o > 0,2 ), podemos modelar a temperatura adimensional na superfície ( r * = R R = 1 ) a partir da equação:

ϴ S * = T S - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o ) J 0 ( ζ 1 r * )

Sendo T S a temperatura na superfície do bastão.

Antes de partir para o Passo 2, devemos procurar as propriedades da pirocerâmica na Tabela A.2 (página 627) para a temperatura média de T m e d = 900   K + 600   K 2 = 750   K . Interpolando os valores apropriados na Tabela, chegamos a:

ρ =   2600 k g m 3 c ´ P = 1100 J k g . K k   =   3,13 W m . K α = k   ρ c ´ P = 1,09 x 10 - 6     m 2 s  

Agora, pra gente não se perder, vamos guardar as propriedades que vamos usar nos próximos passos:

T i = 900   K ,   T ∞ =   300   K   e   T 0 = 600   K R = 20   m m 2 = 10   m m = 0,01   m   h   =   100 W m 2 . K R t , c ' =   0,12   m . K W

Passo 2

Essa questão tem uma “pegadinha” interessante. Ao invés de usarmos o coeficiente de convecção para calcular o número de Biot, devemos calcular um coeficiente global de transferência de calor com a resistência à convecção e a resistência de contato:

U =   1 1 h + R t , c ' ( π D ) = 1 1 100 W m 2 . K + 0,12   m . K W ( π ( 0,020   m ) ) = 57 W m 2 . K

Agora, devemos calcular o número de Biot para o problema:

B i =   U R k =     57 W m 2 . K 0,01   m     3,13 W m . K ≅   0,18  

Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 parao cilindro. Como não temos   B i = 0,18     , devemos fazer uma interpolação entre B i = 0,15 e B i = 0,2 :

B i   = 0,15   →   ζ 1 = 0,5376       C 1 =   1,0365

B i   = 0,2   →   ζ 1 = 0,6170     C 1 =     1,0483

Portanto, interpolando:

B i   = 0,18 →   ζ 1 = 0,5852     C 1 = 1,0436

Vamos deixar o número de Fourier em função de t :

F o = α t R ² =   1,09 x 10 - 6     m 2 s t ( 0,01   m ) ² = 0,0109 t

Vamos substituir os valores que encontramos na equação para a temperatura do eixo central que deduzimos no Passo 1:

ϴ 0 * = 1,0436 exp ⁡ - 0,5852 2 0,0109 t = 1,0436 exp ⁡ - 0,00373 t

Além disso, devemos lembrar que:

ϴ 0 * = T 0 - T ∞ T i - T ∞ =   600   K - 300   K 900   K - 300   K = 0,5

Igualando os dois resultados:

1,0436 exp ⁡ - 0,00373 t =   0,5 → exp ⁡ - 0,00373 t = 0,4791

Vamos aplicar l n em ambos os lados da equação:

ln ⁡ exp ⁡ - 0,00373 t = ln ⁡ 0,4791 → - 0,00373 t = - 0,7358   → t = 197,27   s

Vamo agora calcular o número de Fourier pra confirmar que nossa suposição de tempos longos tá certa:

F o = 0,00373 197,27   s = 0,74 > 0,2

Logo, nossa suposição estava certa :)

Passo 3

Pra finalizar a questão, vamos resolver a letra (b).

Devemos encontrar expressões para temperatura ao longo do tempo para cada uma das seguintes condições de coeficiente de convecção h :

  • Para h = 100 W m 2 . K

    • Primeiro, vamos encontrar a temperatura do centro em função de t:

    T 0 - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o )

    → T 0 ( t ) = 300 + ( 900 - 300 ) 1,0436 exp ⁡ - 0,00373 t

    → T 0 t = 300 + ( 626,16 ) e x p ⁡ ( - 0,00373 t )

    Para a temperatura da superfície em função de t:

    T S - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o ) J 0 ( ζ 1 )

    T S t = 300 + ( 900 - 300 ) 1,0436 exp ⁡ - 0,00373 t J 0 ( 0,5852 )

    função J 0 é a Função de Bessel de Ordem Zero, na Tabela B.4 (página 652). Como não temos J 0 0,5852 , vamos interpolar os valores de J 0 0,5 e J 0 0,6 :

      J 0 0,5 = 0,9385   J 0 10,6 = 0 , 912 0   → J 0 1,6373 = 0,9159

    Logo:

    T 0 t = 300 + ( 573,51 ) e x p ⁡ ( - 0,00373 t )

  • Para h = 500 W m 2 . K

    • Primeiro, devemos calcular o coeficiente global:

    U   =   1 1 h + R t , c ' ( π D ) = 1 1 500 W m 2 . K + 0,12   m . K W ( π ( 0,020   m ) ) = 104,82 W m 2 . K

    Agora, vamos calcular o número de Biot:

    B i =   h R k =     104,82 W m 2 . K 0,01   m         3,13 W m . K ≅     0,3  

    Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 parao cilindro. Para   B i = 0,3   :

    B i   = 0,3   →   ζ 1 = 0,7465     C 1 =     1,0712

    Agora, de maneira análoga ao que fizemos para h = 100 W m 2 . K   , vamos encontrar T 0 ( t ) e T s ( t ) :

    T 0 t = 300 + ( 642,72 ) e x p ⁡ ( - 0,00607 t )

    T S ( t ) = 300 + ( 556,21 ) e x p ⁡ ( - 0,00607 t )

  • Para h = 1000 W m 2 . K

Primeiro, devemos calcular o coeficiente global:

U   =   1 1 h + R t , c ' ( π D ) = 1 1 1000 W m 2 . K + 0,12   m . K W ( π ( 0,020   m ) ) = 117,1 W m 2 . K

Agora, vamos calcular o número de Biot:

B i =   h R k =     117,1 W m 2 . K 0,01   m         3,13 W m . K ≅     0,4  

Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 parao cilindro. Para   B i = 0,4   :

B i   = 0,4   →   ζ 1 = 0 , 8516     C 1 =     1 , 0932

Agora, de maneira análoga ao que fizemos para h = 100 W m 2 . K     e     h = 500 W m 2 . K ,   vamos encontrar T 0 ( t ) e T s ( t ) :

T 0 t = 300 + ( 655,92 ) e x p ⁡ ( - 0,00791 t )

T 0 t = 300 + ( 542,28 ) e x p ⁡ ( - 0,00791 t )

Agora, pra matar de vez essa questão vamos agora traçar o gráfico de temperatura por tempo (de 0 a 300 s) com ajuda do Excel:

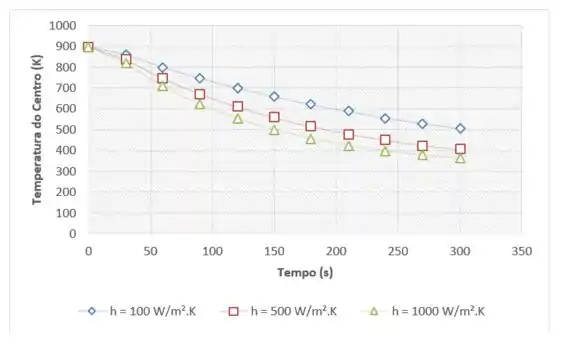
Como podemos ver, quanto maior o coeficiente h , menor é a resistência a transferência de calor por convecção e mais rápido as temperaturas da superfície do centro vai diminuindo.

Fechou? ;)

Resposta

(a) O tempo necessário para a temperatura do centro atingir 600 K é t = 197,27     s .

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Inicia-se a aplicação de um revestimento plástico em painéis de madeira pela deposição de polímero fundido sobre o painel e o posterior resfriamento da superfície do polímero ao submetê-la a uma corre
Uma barra comprida cilíndrica, com 40 mm de diâmetro, fabricada em safira (óxido de alumínio) e inicialmente a uma temperatura uniforme de 800 K, é resfriada subitamente por um fluido a 300 K, que man
Como parte de um processo de tratamento térmico, bastões cilíndricos de aço inoxidável 304 com 100 mm de diâmetro são resfriados a partir de uma temperatura inicial de 500°C pela sua suspensão em um b
Um cilindro comprido com 30 mm de diâmetro, inicialmente a uma temperatura uniforme de 1000 K, é subitamente resfriado pela imersão em um grande banho de óleo que se encontra a uma temperatura constan
Um longo bastão cilíndrico, com 60 mm de diâmetro e propriedades termofísicas iguais a ρ = 8000 kg/m3, c = 500 J/(kg · K) e k = 50 W/(m ·K), encontra-se inicialmente a uma temperatura uniforme e é aqu