Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 20
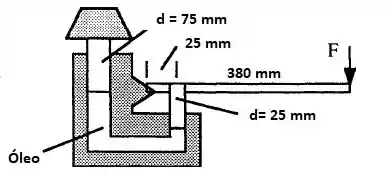
O macaco hidráulico abaixo está cheio com óleo a 8,797 N/m³. Desprezando o peso dos dois pistões, qual a força F necessária na alavanca para suportar o peso de 8.900 N indicado no desenho?
Passo 1
E aí, gente!! Tudo bem? Vamos agora entender direitinho como podemos resolver esse problema de macaco hidráulico que é algo que um dia você precisará usar no seu carro hehe
Primeira coisa que precisamos entender é o que significa aquela unidade de N/m³. Isso nada mais é do que o produto da densidade do óleo com a gravidade, beleza?
Vamos calcular qual é a pressão que esse peso está fazendo?
Passo 2
Sabe-se que essa pressão exercida sobre o óleo deve ser no mínimo igual a todas as forças que estão atuando na outra ponta para que haja sustentação do peso.
As forças que atuam como podemos ver é o torque e o uma força P na região de comprimento 25 mm. Onde o torque está atuando a 380 mm + 25 mm = 405 mm de distância de onde a força F está sendo atuada.
Passo 3
Como estamos em equilíbrio, temos que esse somatório das forças atuando devem somar zero, concorda?
Observe que esse sinal negativo da força P atuando na região de 25 mm é porque ela literalmente faz uma força contrária ao torque exercido.
TCHARAMMMM, OLHA AGORA A MÁGICA!!!
Podemos então escrever que:
Lembrando que essa distância “d” é a distância de onde está sendo aplicado a força até o ponto de torque.
Beleza, mas qual é a força P que está atuando ali naquela região de 25 mm de comprimento?
Note que essa força “P” nada mais é do que o próprio peso que atua naquela região, portanto a área que sustenta esse peso é de , correto? E a pressão de óleo foi calculada anteriormente. Se você então substituir na equação de P, terá o valor de P = 987 Pa x m².
Portanto, F = 987/0,405 = 2,43 kPa/m
Resposta
F = 2,43 kPa/m