Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 137

A mangueira no Problema 8.135 é trocada por uma mangueira mais larga, de diâmetro 25 mm (com o mesmo comprimento e rugosidade). Considerando uma profundidade da piscina de 1,5 m, qual será a nova velocidade média e a nova vazão?

Passo 1

Oi pessoal, tudo bem ?

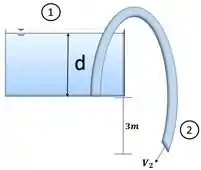
Bem, vamos relembrar o esboço um pouco mal feito da piscina com a mangueira !!

As mudanças que o enunciado propõe são:

  1. A profundidade da piscina d já é indicada no enunciado;
  2. A velocidade V 2 agora é o nosso objeto de estudo;
  3. Consequentemente a vazão Q   também se torna objeto de estudo.

Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:

P 1 ρ ∙ g +   α ∙ V 1 2 2 g + z 1 =   P 2 ρ ∙ g +   α ∙ V 2 2 2 g + z 2   +   h p

Consideremos α = 1 ;

P 2 = P a t m = P 1 ;

Como a piscina é um reservatório, consideramos a velocidade V 1 = 0 ;

Podemos reescrever a diferença z 1 - z 2 = d + Δ z .

As perdas de carga serão representadas pela eq da perda de carga maior, e a eq perda de carga menor:

h p = f V ² L 2 g D + K V 2 2 2 g              

K   refere-se ao coeficiente de perda de carga na entrada da mangueira, que recebe o valor de K = 0,5 (Tabela 8.2) .

Podemos admitir também que V 2 = V

Passo 2

Agora, devemos simplificar a equação da energia:

d = V 2 2 g f L D + K + 1 - Δ z

Ao isolar a nova icógnita V, temos:

V = 2 g Δ z + d f L D + K + 1   ( 1 )

Da tabela A.7, temos o valor da viscosidade cinemática da água, para a descoberta do Re do problema:

Sendo υ = 1,01 * 10 - 6 (para 20 0 C )

R e = V D υ     ( 2 )

Sabemos também que:

1 f = - 2 ∙ log ⁡ e D 3,7 + 2,51 R e ∙ f     ( 3 )

Passo 3

As equações 1, 2 e 3 formam um conjunto de equações simultâneas para V ,   R e   e   f , que podemos resolver iterativamente (por meio do excel, ou outra ferramenta computacional):

  1. Primeiro, fazendo uma primeira suposição para o valor de f:

    2. f = 0,1

    Então, pela iteração:

    V = 0,852 m s         e       R e = 2,13 * 10 4

  2. Utilizando o mesmo valor de Re encontrado, resolve-se a equação 3 e encontramos o valor de f=0.0382.

    3. Repetindo a iteração:

    V = 1,37 m s         e       R e = 3,41 * 10 4

  3. Novamente, utilizando o mesmo valor do novo Re encontrado, resolve-se a equação 3 e encontramos o valor de f=0.0371.

    4. Repetindo a iteração:

    V = 1,38 m s         e       R e = 3,46 * 10 4

  4. Fazendo a mesma iteração, encontramos novamente o valor de f=0,0371. Então, pode-se perceber que há uma convergência.

Resposta

Portanto, partindo desse pressuposto, temos que:

V = 1,38 m s

E, consequentemente:

Q = V π D 2 4           →       Q = 6,79 * 1 0 - 4 m 3 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema de tubos de ferro fundido conduzindo água é constituído de um trecho de 46m , após o qual o escoamento se divide em dois ramais de 46m cada um, que se juntam em um trecho final de 46m . Per
Por que a temperatura da água do chuveiro muda quando a descarga do vaso sanitário é acionada? Esboce as curvas de pressão para os sistemas de suprimento de água quente e de água fria para explicar o
Determine as vazões volumétricas Q 0 ,Q 1 ,Q 2eQ 4 se o ramal 3 for bloqueado.
Água a 20°C escoa por um tubo inclinado de 8 cm de diâmetro. Nas seções A e B são obtidos os seguintes dados: pA = 186 kPa, VA = 3,2 m/s, zA = 24,5 m, pB =260 kPa, VB 5 3,2 m/s e zB =9,1 m. Qual é o s
Um líquido leve (rho = 950 kg/m3) escoa a uma velocidade média de 10 m/s por um tubo liso de 5 cm de diâmetro. A pressão do fluido é medida em intervalos de 1 m ao longo do tubo, como se segue:Calcule