Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 66
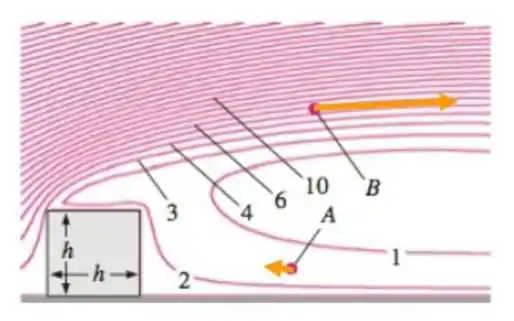
A média no tempo de um escoamento bidimensional turbulento, incompressível, sobre um bloco quadrado de dimensão h = 1 m é modelado com um aplicativo comercial de dinâmica dos fluido computacional (CFD). Uma vista ampliada das linhas de corrente (contornos de função corrente constante) é mostrada na Figura P9-66. O fluido é ar à temperatura ambiente. Note que os contornos de função corrente compressível constante são mostrados na Figura P9-66, apesar do próprio escoamento ser aproximado como incompressível. Os valores de estão em unidades de kg/m.s.
(a) Desenhe uma seta no gráfico para indicar a direção e intensidade relativa da velocidade no ponto A. Repita para o ponto B.
(b) Qual é a velocidade aproximada do ar no ponto B? (O ponto B está entre as linhas de corrente 5 e 6 na Figura P9-66).
Passo 1
Fala aí, tudo bem? Vem comigo que eu vou te ajudar a interpretar o enunciado e resolver esse problema.
Nessa questão, a gente tem um bloco quadrado de lado por onde escoa ar sendo modelado em um programa CFD, e por isso ele tem suas linhas de corrente à mostra.
A questão nos pede, no primeiro momento, pra indicar na figura a direção e intensidade relativa dos vetores de velocidade em dois pontos indicados. Pra isso, a gente deve lembrar a definição da função de corrente incompressível:
Isso significa que está intimamente ligado à velocidade do escoamento.
Por fim, a gente vai calcular a velocidade aproximada no ponto A indicado na figura. Pra isso, a gente tem que usar a seguinte equação pra cálculo velocidade em um ponto entre duas linhas de corrente incompressíveis:
Sendo e os valores das funções de corrente incompressível no entorno do ponto e a distância entre as linhas de corrente em torno desse ponto, e é a densidade do ar a temperatura ambiente (C).
Pronto, agora podemos ir pros próximos passos e resolver essa questão juntos!
Passo 2
Vamos começar resolvendo primeiro a letra (a), representando os vetores velocidade nos pontos indicados.
Primeiro, temos que definir a direção dos vetores de velocidade nos pontos A e B.
Pra isso, vamos usar a regra chamada de “convenção do lado esquerdo”, que diz que a função corrente aumentará do lado esquerdo perpendicular à direção do escoamento.
Além disso, a gente tem que definir a magnitude relativa desses vetores. Como o ponto B está em linhas de corrente de valor maior, ele tem uma magnitude do vetor de velocidade maior do que aquele no ponto A.
Se a gente medir com uma régua a distância entre as linhas de corrente em torno dos pontos, a gente vai perceber que as linhas em torno do ponto A estão distantes quase em nossa escala. As linhas em torno do ponto B, no entanto, estão distantes cerca de
Ou seja, a intensidade do vetor velocidade no ponto B pode ser representada como sendo 5 vezes maior que aquele no ponto A:
Passo 3
Pra finalizar a questão, vamos agora resolver a letra (b).
Temos que calcular velocidade do ponto B, que está entre as linhas de corrente 5 e 6.
Mas antes, precisamos descobrir a distância entre as linhas de corrente em torno do ponto. Pra isso, basta a gente usar uma régua e medir a distância entre as linhas de corrente 5 e 6, passando pelo ponto B. Fazendo isso, a gente tem que .
Agora, vamos substituir os valores na equação pra velocidade que eu te mostrei no Passo 1:
Pronto, matamos a questão juntos!
Resposta
(a) Os vetores de velocidade nos pontos A e B são demonstrado abaixo:
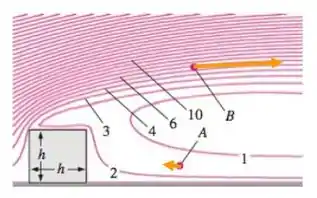
(b) A velocidade aproximada do ar no ponto B é .
.