Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 102
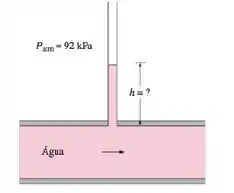
Um tubo de vidro é anexado a um cano de água, como mostra a figura. Se a pressão da água na parte inferior do tubo for de a pressão atmosférica local for de determine até qual altura a água subirá no tubo, em Considere naquele local e tome a densidade da água como
Passo 1
Fala aí galerinha do responde aí, vamos para mais uma questão para garantir aquele notão na prova de Mecflu. Primeiramente, sabemos que:
Também sabemos que:
Como a área do tubo de vidro é constante, temos que:
Logo, a massa de água será:
Passando para volume:
Como o tubo é cilíndrico, temos que:
Logo:
Onde a área da base é dada em metros quadrados e em metros.
Resposta
Exercícios de Livros Relacionados
Uma linha de gasolina está conectada a um medidor de pressão através de um manômetro duplo em U, como mostra a figura. Se a leitura da pressão manométrica for de 370 k P a , determine a pressão manomé
Infusões intravenosas em geral são movidas pela gravidade, pendurando-se a garrafa de fluido a uma altura suficiente para contrabalancear a pressão do sangue na veia e forçar o fluido a entrar no corp
O barômetro básico pode ser usado como um dispositivo de medição da altitude em aviões. O controle de terra reporta uma leitura barométrica de 753m m H g enquanto a leitura do piloto é de 690m m H g .
Determine a quantidade máxima de carga, em k g , que o balão descrito no problema 3 - 95 pode transportar.
A pressão atmosférica média na terra é aproximada como uma função da altitude pela relação P a t m = 101,325 1 - 0,02256 z 5,256 , onde P a t m é a pressão atmosférica em k P a e z é a altitude em k m