Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 41

Como mencionado na Seção 4.10, o perfil de velocidade para escoamento laminar entre duas placas, como na Figura P4.41, é

u = 4 u m á x y h - y h 2                                           v = w = 0  

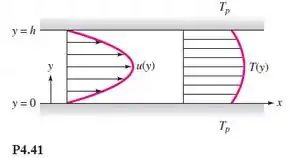
Se a temperatura em ambas as paredes é T p , use a equação da energia para escoamento incompressível (4.75) para resolver a distribuição de temperatura T(y) entre as paredes para o escoamento permanente.

Passo 1

E vamos para mais uma! Simbora!

Considerando T = T ( y ) e usando a equação de energia tendo o nosso perfil de velocidade, vamos ter:

ρ c p d T d t = k d 2 T d y 2 + μ d u d y 2  

ρ c p 0 = k d 2 T d y 2 + μ 4 u m á x h 2 h - 2 y 2

d 2 T d y 2 = - 16 μ u m á x 2 k h 4 ( h 2 - 4 h y + 4 y 2 )

Integrando, teremos:

d T d y = - 16 μ u m á x 2 k h 4 h 2 y - 2 h y 2 + 4 y 3 3 + C 1

Quando y = h 2 , teremos d T d y = 0 , assim, C 1 = - h 3 6 . Substituindo e integrando novamente, teremos:

T = - 16 μ u m á x 2 k h 4 h 2 y 2 2 - 2 h y 3 3 + y 4 3 + C 1 y + C 2

Se, T = T w quando y = 0 e quando y = h , teremos que C 2 = T w , assim, teremos a solução sendo:

T = T w + 8 μ u m á x 2 k y 3 h - y 2 h 2 + 4 y 3 3 h 3 - 2 y 4 3 h 4

Resposta

T = T w + 8 μ u m á x 2 k y 3 h - y 2 h 2 + 4 y 3 3 h 3 - 2 y 4 3 h 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a velocidade do ar no tubo é 228,6m / s , utilize a medição do manômetro de mercúrio na Figura P9.25 para calcular a pressão estática absoluta no duto em kPa.
Para escoamento de gás a baixa velocidade (quase incompressível), a pressão de estagnação pode ser calculada a partir da equação de Bernoulli: p 0 = p + 1 2 ρ V 2 Para velocidades subsônicas mais alta
O Problema 9.37 é ideal para um projeto de formatura ou como um problema combinado de laboratório e computador, como se descreve na Referência 27, Seção 8.6. No experimento de laboratório de Bober e K
Faça uma análise exata de volume de controle do processo de esvaziamento na Figura P9.37, admitindo um tanque isolado com energias cinética e potencial desprezível dentro dele. Admita escoamento críti
Um pneu de bicicleta está cheio de ar a uma pressão absoluta de 169,12 kPa e sua temperatura interna é 30,0 °C. Suponha que a válvula quebre e o ar comece a escapar para fora do pneu na atmosfera ( p