Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 73
A água entra em uma turbina hidráulica por meio de um tubo com de diâmetro a uma vazão de e sai através de um tubo com de diâmetro. A queda de pressão na turbina é medida por um manômetro de mercúrio como Para uma eficiência combinada de turbina-gerador de , determine o resultado total de potência elétrica. Despreze o refeito dos fatores de correção da energia cinética.
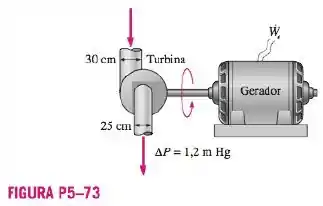
Passo 1
Temos a entrada da turbina, consideremos a entrada como , passando água e temos que determinar a potencial total de saída, adotaremos saída como (2).
Vamos assumir que o fluxo é constante e incompressível, como o enunciado nos deu eficiência da turbina, temos que as perdas totais o nosso , pois, as perdas já estão contabilizadas na eficiência da turbina. Como ele pediu para desprezar o fator de correção teremos .
Para determinar a potencial total de saída temos que saber a carga total de turbina utilizada, logo, escrevendo a equação do balanço de energia temos:
Como nosso objetivo é determinar carga da turbina, vamos isola-la:
Perceba que falta, para determinar o resultado, a diferença de pressão e as velocidades.
Passo 2
Vamos lá, precisamos determinar as velocidades.
Como o fluxo é conhecido de constante, e temos que para de terminar a velocidade basta dividir o fluxo pela área:
Repetindo o mesmo para :
Passo 3
Para determinar a pressão, vamos dar uma olhada na coluna de mercúrio, enunciado nos diz “A queda de pressão na turbina é medida por um manômetro de mercúrio como ”. Temos uma variação de pressão por colunas de mercúrio:
Aplicando a lei de pascal:
Substituindo valores:
Passo 4
Substituindo todos os cálculos feitos na equação da carga de turbina:
Passo 5
Agora para finalmente determinarmos a potencia elétrica final, basta aplicamos a formula, temos:
Como , temos: