Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 1
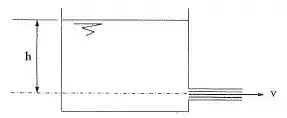
Determinar a velocidade do jato do líquido no orifício do tanque de grandes dimensões da figura. Considerar fluido ideal.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Como o reservatório é de grandes dimensões, temos que fazer algumas considerações para que possamos fazer os cálculos. No caso de reservatórios de grandes dimensões, o regime é permanente e o nível é considerado constante.
Vamos considerar o seguinte diagrama com o ponto horizontal de referência:
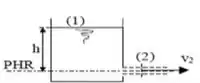
A equação de bernoulli é dada por:
Vamos avaliar cada termo. é a altura do ponto ao plano de referência horizontal:
Como o reservatório é muito grande, consideramos a velocidade do líquido no ponto igual a zero.
Como os dois pontos estão ao ar livre as pressões manométricas se anulam.
A parcela diz respeito a uma máquina, bomba ou turbina. Como não temos nenhuma máquina no problema, temos que:
.
Como o fluido é ideal, não há perda de carga logo:
Passo 2
Feitas as devidas análises, podemos substituir os termos da equação de bernoulli:
Portanto:
Como não há perdas o coeficiente de correção .
Substituindo os valores conhecidos, temos que:
A velocidade de saída, será: