Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 94

Um misturador rotativo consiste em dois semitubos de 1 m de comprimento girando em torno de um braço central, como na Figura P7.94. Usando o arrasto da Tabela 7.2, deduza uma expressão para o torque T necessário para acionar o misturador à velocidade angular Ω em um fluido de massa específica r. Suponha que o fluido seja água a 20°C e a potência máxima de acionamento disponível seja 20 kW. Qual a velocidade de rotação máxima Ω, em rpm?

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos um misturador rotativo de dois semitubos de comprimento R = 1   m ,diâmetro D = 0,05   m de velocidade angular Ω funcionando em água a 20 ° C , com massa específica ρ = 998   k g / m ³ e viscosidade μ = 1 × 10 - 3   P a ∙ s .

Essa rotação do misturador gera um torque T com uma potência máxima de acionamento P = 20   k W . O enunciado nos pede pra calcular a velocidade de rotação máxima Ω , e pra isso usaremos essa relação entre a potência e o torque:

P = T Ω

Nos próximos passos, iremos encontrar uma expressão para o torque T e iremos calcular a velocidade de rotação.

Então vem comigo pra gente resolver esse problema junto!

Passo 2

Em primeiro lugar, vamos encontrar uma expressão para o torque T . Pra isso, vamos integrar a força de arrasto da seguinte maneira:

T =   2 ∫ r d F A

Note que o “2” na frente da integral indica que o torque leva em conta a força de arrasto nos dois semitubos.

Podemos considerar a diferencial da força de arrasto igual a:

d F A = C A ρ 2 ( Ω r ) ² D d r

Substituindo na integral:

T =   2 ∫ 0 R C A ρ 2 Ω 2 D r 3 d r = C A ρ Ω 2 D R 4 4

Passo 3

Antes de resolver a questão, devemos encontrar o coeficiente de arrasto C A . Ele podem ser encontrados na Tabela 7.2, Página 493 , como na imagem:

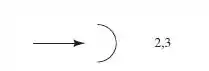
Ou seja, C A = 2,3 .

Podemos substituir tudo isso na equação pra potência que eu te mostrei no Passo 1:

P = T Ω → 20000   W = 2,3 998 k g m 3 Ω 2 0,05   m 1 m 4 4 Ω

Isolando e resolvendo a equação cúbica pra velocidade de rotação:

Ω ³ = 697

Ω = 8,87 r a d s = 84,7   r p m

Resposta

A velocidade de rotação máxima é Ω = 84,7   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para medir o arrasto de uma pessoa em posição ereta, sem violar protocolos de segurança, um manequim do tamanho da pessoa é fixado à extremidade de uma barra de 6 m e posto para girar a Ω = 80 rpm, co
Aplique o Problema 7.61 a um filtro que consiste em um pacote de 250 fibras por centímetro quadrado, cada qual com 300 μm de diâmetro, no plano da Figura P7.61. Para o ar a 20oC e 1 atm escoando a 1,5
Suponha que uma partícula de poeira radioativa se assemelhe a uma esfera de massa específica 2.400 kg/m3. Quanto tempo, em dias, levará tal partícula para descer de uma altitude de 12 km até o nível d
Uma esfera pesada fixada em uma corda se deslocaria um ângulo θ quando imersa em uma corrente de velocidade U, como na Figura P7.80. Deduza uma expressão para u em função das propriedades da esfera e
Um paraquedas típico do Exército norte-americano tem um diâmetro projetado de 8,5 m. Para uma carga total com massa de 80 kg, (a) qual é a velocidade terminal resultante na altitude padrão de 1.000 m?