Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 78

Aplique o Problema 7.61 a um filtro que consiste em um pacote de 250 fibras por centímetro quadrado, cada qual com 300 μm de diâmetro, no plano da Figura P7.61. Para o ar a 20oC e 1 atm escoando a 1,5 m/s, calcule a queda de pressão se o filtro tem 5 cm de espessura.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos um filtro com 250   f i b r a s / c m ² , cada uma delas com diâmetro D = 0 , 000 3   m . Ar escoa nesse filtro a 1   a t m e 20 ° C , com velocidade V = 1,5   m / s .

A questão nos pede para calcular a queda de pressão se o filtro tem espessura L = 0,05   m .

Pra isso, vamos utilizar a equação deduzida no Problema 7.61:

∆ P f i l t r o = N L C A ρ 2 V ² D

Sendo: N = 250 / c m ² = 2,5 × 10 6 / m ² o número de fibras por unidade de área e C A é o coeficiente de arrasto.

Pra resolver esse problema, devemos lembrar que para o ar a temperatura ambiente teremos uma massa específica de ρ = 1,2   k g / m ³ e viscosidade μ = 1,8 × 10 - 5 k g / m ∙ s .

Agora vem comigo pra gente resolver esse problema!

Passo 2

Nesse Passo 2, vamos calcular o coeficiente de arrasto C A para cada uma das fibras.

Pra isso, antes vamos calcular o número de Reynolds para o escoamento:

R e D = ρ V D μ = 1,2   k g / m ³ 1,5   m / s 0 , 000 3   m 1,8 × 10 - 5 k g / m ∙ s = 3 0

Considerando um cilindro curto liso com L D = ∞   , vamos na Figura 7.16 (a), na página 492, entramos com o valor de Reynolds e obtemos:

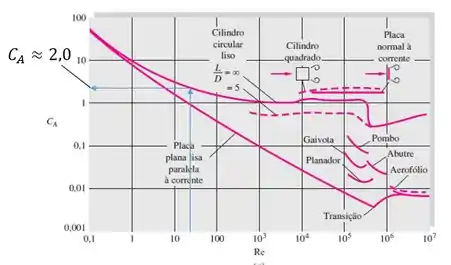
O coeficiente de arrasto encontrado foi de C A ≈ 2,0 .

Passo 3

Pra finalizar a questão, vamos calcular a queda de pressão no filtro.

Vamos então substituir as grandezas que demonstramos nos passos anteriores:

∆ P f i l t r o = 2,5 × 10 6 / m ² ( 0,05   m )   ( 2,0 ) 1,2   k g / m ³ 2 ( 1,5   m / s ) ² ( 0,0003   m )

∆ P f i l t r o = 101,25   P a

Pronto, matamos a questão juntos!

Resposta

A queda de pressão no filtro é ∆ P f i l t r o = 101,25   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Num viscosímetro de esfera, uma esfera de aço de massa específica ρ = 7.800k g / m 3 e diâmetro 1m m afunda num líquido de massa específica ρ = 800k g / m 3 , com uma velocidade limite de 2c m / s . C
Determinar a relação entre a velocidade constante de subida de uma bolha de ar de diâmetro 1mm dentro da água e a velocidade constante de descida de uma gota de água de mesmo diâmetro no ar. Dados: ρ
Uma placa de 0,9 m x 1,2 m move-se com 13,2 m/s em ar parado, com uma inclinação de 12º com a horizontal. Sendo C a = 0,17 ; C s = 0,72 ; ρ = 1,2k g / m 3 ; A=área de referência = área da placa, deter
Um avião F4 é desacelerado após a aterrissagem por paraquedas duplos disparados da traseira. Cada um dos paraquedas tem 3,7m de diâmetro. O F4 pesa 142.400 N e aterrissa a 160 m/s. Estime o tempo e a
Um misturador rotativo é construído com dois discos circulares, conforme mostrado. O misturador é acionado a 60 rpm dentro de um grande vaso contendo uma solução de salmoura (SG = 1,1). Despreze o arr