Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 30
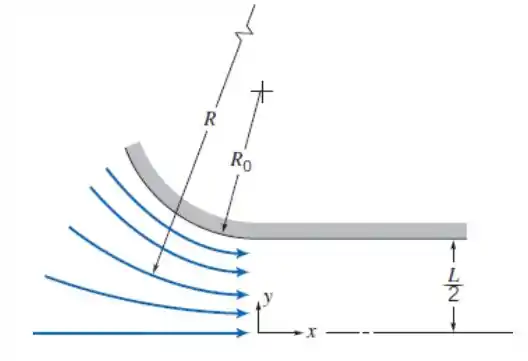
Para modelar a distribuição de velocidade na seção curva de entrada de um túnel de vento, o raio de curvatura das linhas de corrente é expresso como R = LR0/2y. Em primeira aproximação, considere que a velocidade do ar ao longo de cada linha de corrente é V = 10 m/s. Encontre uma expressão e trace o gráfico da distribuição de pressão de y = 0 até a parede do túnel em y = L/2, se a pressão manométrica na linha de centro for 50 kPa, L = 75 mm e R0 = 0,2 m. Avalie o valor de V para o qual a pressão estática na parede se torna igual a 35 kPa.
Passo 1
Pessoal, no item 6.2 do livro são deduzidas as equações de Euler em coordenadas de linha de corrente, que é o caso desta questão. Para escoamento em regime permanente em um plano horizontal, a equação de Euler normal a uma linha de corrente vale:
Onde n é a direção normal.
No momento da entrada, o vetor normal está na direção vertical, então:
Substituindo o valor de R, temos:
Passo 2
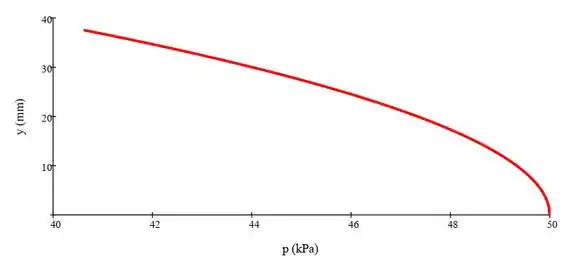
Para encontrar a distribuição de pressão, basta integrar a expressão acima:
Onde é a pressão na linha de centro. Para encontrar a pressão na parede do túnel (y=L/2), basta substituir os valores:
Passo 3
Considerando a pressão estática da parede igual35 kPa, vamos encontrar a velocidade, isolando na equação anterior:
Substituindo os valores: