Um ventilador de caixa está no chão em uma sala muito grande (Figura P10-2C). Identifique as regiões do campo de escoamento que podem ser aproximadas como estáticas. Identifique as regiões nas quais a aproximação irrotacional pode ser apropriada. Identifique as regiões onde a aproximação da camada limite pode ser apropriada. Finalmente, identifique as regiões nas quais a equação completa de Navier-Stokes provavelmente precisa ser resolvida (isto é, regiões onde nenhuma aproximação é apropriada).
Passo 1
Fala Galera!!!
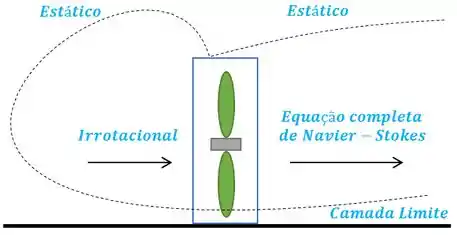
Para resolver essa questão, podemos fazer o seguinte esquema para o processo descrito no problema mostrando as regiões do campo de escoamento.
Passo 2
Com base no esquema feito acima, podemos dizer que quando o ventilador gira, uma camada limite é formada ao longo do piso, a montante e a jusante do ventilador.
Na jusante do ventilador, o fluxo é principalmente turbulento, assim, nenhuma das aproximações pode ser feita e, portanto, a equação de Navier-Stokes completa deve ser resolvida nessa região, porque nenhum dos termos pode ser eliminado da equação.
O fluxo na região a montante do ventilador é irrotacional, exceto muito próximo do piso. Portanto, a aproximação irrotacional é apropriada e o termo correspondente na equação de Navier-Stokes pode ser eliminado.
Na região a montante e muito acima do ventilador, o fluxo é quase estático. Portanto, o fluxo pode ser aproximado como estático e o termo correspondente na equação de Navier-Stokes pode ser eliminado.
Resposta
A resposta dessa questão está descrita nos passos acima, pois fica mais fácil de entender ao ver o esquema feito no passo 1.