Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 20

Mostre que a força exercida por um jato de líquido em um bocal fixo quando ele sai com uma velocidade V é proporcional a V 2 ou, altenativamente, a m ˙ 2 .

Passo 1

O enunciado quer que a gente mostre que a força F (que o fluido que entra no bocal aplica sobre o bocal fixo) é proporcional a V 2 ou m ˙ 2 . V é a velocidade do líquido que sai do bocal. m ˙ é a vazão mássica de líquido através do bocal. O primeiro passo para demonstrar isso é escolhendo um volume de controle. Como queremos informações sobre o bocal, escolhemos um volume de controle que engloba o bocal.

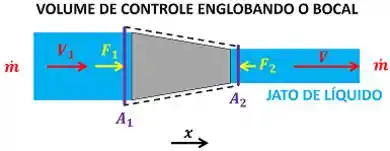
V 1 é a velocidade do jato de líquido entrando no bocal pela área A 1 . Esse escoamento de líquido entrando no bocal exerce uma força F 1 sobre o volume de controle. V é a velocidade de líquido saindo do bocal pela área A 2 . Esse escoamento de líquido saindo do bocal exerce uma força F 2 sobre o volume de controle. F 2 e F 1 são opostas. Logo, a força total F do jato sobre o bocal vale:

F = F 1 - F 2

Mostrar que a força F é proporcional a V 2 ou m ˙ 2 é a mesma coisa que descobrir uma fórmula para F em função de V 2 e outra em função de m ˙ 2 . Para encontrar essas fórmula, precisamos primeiro usar a segunda lei de Newton (equação da quantidade de movimento) no volume de controle acima!

Passo 2

Agora que escolhemos o volume de controle, podemos usar a segunda lei de Newton nesse volume de controle. Para simplificar, o escoamento do volume de controle é considerado como sendo um escoamento em regime permanente. Como estamos interessados apenas na sua aceleração horizontal (ao longo do eixo x ), usaremos apenas a equação de quantidade de movimento (segunda lei de Newton) relativa ao eixo x apenas.

Além disso, o volume de controle possui apenas uma corrente de fluido entrando horizontalmente e uma corrente saindo horizontalmente. Por causa de todos esses fatores, podemos usar a equação 6 - 27 .

∑ F x = m ˙ ⋅ β 2 ⋅ V 2 , x - β 1 ⋅ V 1 , x

onde ∑ F x é o somatório das forças horizontais (no eixo x ) sobre o volume de controle, m ˙ é a vazão mássica do jato entrando e saindo do volume de controle. β 1 é o fator de correção para o escoamento que entra no volume de controle. β 2 é o fator de correção para o escoamento que sai do volume de controle. V 1 , x é a velocidade do jato no eixo x que entra no volume de controle. V 2 , x é a velocidade do jato no eixo x que sai do volume de controle.

Esta é a equação de quantidade de movimento no eixo x (segunda lei de Newton) para um escoamento em regime permanente, com uma corrente entrando e outra saindo. No próximo passo descobriremos quanto vale cada termo dessa fórmula.

Passo 3

Como foi falado anteriormente, a força total exercida sobre o volume de controle é igual a F . Logo:

∑ F x = F

Se nós considerarmos que o escoamento é incompressível (com densidade ρ constante), podemos calcular m ˙ pela equação abaixo.

m ˙ = ρ ⋅ V ⋅ A 2

Além disso, pela equação 5 - 21 do livro, conseguimos calcular a velocidade V 2 em função de V .

ρ ⋅ V 1 ⋅ A 1 = ρ ⋅ V ⋅ A 2       ⟹       V 1 = V ⋅ A 2 A 1

Substituindo todos esses dados na segunda lei de Newton, achamos:

∑ F x = m ˙ ⋅ β 2 ⋅ V 2 , x - β 1 ⋅ V 1 , x       ⟹       F = ρ ⋅ V ⋅ A 2 ⋅ β 2 ⋅ V - β 1 ⋅ V 1

F = ρ ⋅ V ⋅ A 2 ⋅ β 2 ⋅ V - β 1 ⋅ V ⋅ A 2 A 1       ⟹       F = ρ ⋅ V 2 ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1

A fómula acima é a prova de que F é proporcional a V 2 .

Passo 4

Agora vamos achar a fórmula de F em função de m ˙ 2 para provar que F é proporcional a m ˙ 2 .

Para isso, vamos usar a fórmula que acabamos de deduzir. Para transformar essa fórmula de V 2 em fórmula de m ˙ 2 , é necessário lembrar que:

ρ ⋅ V ⋅ A 2 = m ˙

V = m ˙ ρ ⋅ A 2

Substituindo essas duas equações na fórmula de F :

F = ρ ⋅ V 2 ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1         ⟹     F = ρ ⋅ V ⋅ A 2 ⏟ m ˙ ⋅ V ⏟ m ˙ ρ ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1

F = m ˙ ⋅ m ˙ ρ ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1       ⟹       F = m ˙ 2 ρ ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1

A fómula acima é a prova de que F é proporcional a m ˙ 2 .

Resposta

F = ρ ⋅ V 2 ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1

F = m ˙ 2 ρ ⋅ A 2 ⋅ β 2 - β 1 ⋅ A 2 A 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The horizontal lawn sprinkler in Fig. P3.149 has a waterflow rate of 4.0 gal/min introduced vertically through thecenter. Estimate (a) the retarding torque required to keepthe arms from rotating and (
Steam enters a horizontal turbine at 350 lbf/in2 absolute,5808C, and 12 ft/s and is discharged at 110 ft/s and 258Csaturated conditions. The mass fl ow is 2.5 lbm/s, and theheat losses are 7 Btu/lb of
A fire hose, with a 2-in-diameter nozzle, delivers a waterjet straight up against a ceiling 8 ft higher. The force on theceiling, due to momentum change, is 25 lbf. Use Bernoulli’sequation to estimate
A large commercial power washer delivers 21 gal/min ofwater through a nozzle of exit diameter one-third of aninch. Estimate the force of the water jet on a wall normal tothe jet.
Water flows steadily through the box in Fig. P3.63. Average velocity at all ports is 7 m/s. The vertical momentum force on the box is 36 N. What is the inlet mass flow?