Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 21
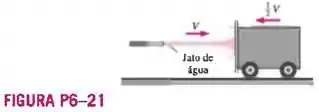
Um jato d’água horizontal com velocidade constante é imposto normalmente a uma placa plana vertical e se espalha nas laterais no plano vertical. A placa se move na direção da entrada do jato d’água com velocidade . Se uma força é necessária para manter a placa fixa, quanta força é necessária para mover a placa na direção do jato d’água?
Passo 1
O enunciado quer saber quanto vale a força necessária para aproximar a placa do bocal com uma velocidade . Em outras palavras, temos que descobrir quanto vale em função de , sendo é a força necessária para manter a placa parada. O primeiro passo para achar a fórmula de é escolher qual é o volume de controle. Como o enunciado quer saber sobre a força aplicada na placa, nós vamos supor que o volume de controle é a região do espaço que engloba a parte do jato colidindo com a placa e a placa. A figura abaixo mostra o volume de controle.
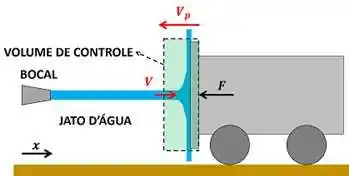
é a velocidade do jato de água que atravessa o volume de controle em relação ao chão e é a velocidade da placa. é a força que a placa exerce sobre o jato. O volume de controle se movimenta junto com a placa. Por isso, a velocidade do volume de controle é igual à velocidade da placa .
Passo 2
Agora que escolhemos o volume de controle, podemos usar a segunda lei de Newton nesse volume de controle. Como a velocidade do jato é constante, o escoamento do volume de controle é considerado como sendo um escoamento em regime permanente.
Como estamos interessados apenas nas forças horizontais (do eixo ), usaremos apenas a equação de quantidade de movimento (segunda lei de Newton) relativa ao eixo apenas. Além disso, o volume de controle possui apenas uma corrente de fluido entrando horizontalmente nele. Por causa de todos esses fatores, podemos usar a equação .
onde é o somatório das forças horizontais (no eixo ) sobre o volume de controle, é a vazão mássica do jato d’água entrando no volume de controle. é o fator de correção para o escoamento que entra no volume de controle. é o fator de correção para o escoamento que sai do volume de controle. é a velocidade relativa do jato no eixo em relação ao volume de controle móvel. é a velocidade relativa da água no eixo que colidiu com a placa.
Esta é a equação de quantidade de movimento no eixo (segunda lei de Newton) para um escoamento em regime permanente, com uma corrente entrando e outra saindo. No próximo passo descobriremos quanto vale cada termo dessa fórmula.
Passo 3
Pela figura acima, a força parece ser a única força sobre o volume de controle no eixo . Mas você poderia se perguntar se a força da pressão do jato e a força da pressão atmosférica também não contam.
Elas existem, mas a pressão de um jato na atmosfera é muito próxima da pressão atmosférica . Logo, a força da pressão do jato se cancela com a força da pressão atmosférica. Por causa disso, vale:
O sinal de menos está presente na fórmula, porque a força está no sentido negativo de .
Além disso, os fatores de correção e valem para jatos!
é a componente horizontal da velocidade relativa do jato em relação ao volume de controle. é a velocidade do jato em relação ao chão mais a velocidade do volume de controle em relação ao chão , porque e estão em sentidos opostos.
é a componente horizontal da velocidade relativa da água que sai do volume de controle. Como a água sai do volume de controle apenas com velocidades verticais, vale zero.
Por fim, a vazão mássica do jato d’água entrando no volume de controle vale:
onde é a massa específica da água e é a área da superfície de controle através da qual o jato passou.
Substituindo a equação de na fórmula de encontramos:
Passo 4
Substituindo todos esses dados na segunda lei, encontramos uma fórmula para a força .
Como a velocidade da placa vale zero, quando uma força é aplicada sobre ela, a força vale:
Como a fórmula de em função de foi deduzida para o caso geral em que a placa tinha uma velocidade , podemos usar essa mesma fórmula para calcular a força .
No entanto, quando uma força é aplicada sobre a placa, ela se move a no sentido do bocal. Logo: