Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 43

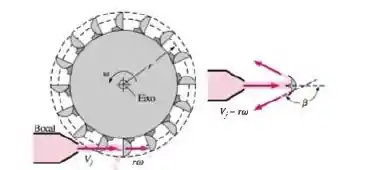
As turbinas de Pelton normalmente são usadas nas usinas hidrelétricas para gerar energia elétrica. Nessas turbinas, um jato à alta velocidade de V j é aplicado sobre as pás, forçando a roda a girar. As pás revertem a direção do jato, e o jato sai da pá fazendo um ângulo β com a direção do jato, como mostra a Figura . Mostre que a potência produzida por uma turbina de Pelton com raio r girando de forma estacionária a uma velocidade angular ω é W ˙ e i x o = ρ ω V ˙ ( V j - ω r ) ( 1 - cos ⁡ β ) , onde ρ é a densidade e V ˙ é a taxa de escoamento de volume do fluido. Obtenha o valor numérico para ρ = 1000 k g m 3 ,   r = 2   m ,   V ˙ = 10 m 3 s ,   n ˙ = 150   r p m ,   β = 160 °   e   V j = 50 m s .

Passo 1

Bora lá! Pra começar a gente precisa de achar a velocidade relativa entre V j e a velocidade do jato que volta!

V r = V j - r ω

Onde ω pode ser calculado por:

ω = 2 π n ˙

Temos um sistema permanente, então:

∑ M = ∑ s a í d a r m ˙ V - ∑ E n t r a d a r m ˙ V

Aplicando para achar o momento do eixo:

- M e i x o = r m ˙ V r cos ⁡ β - r m ˙ V r

Lembrando que tudo que é horário é negativo, beleza? Agora vamos dar uma organizadinha nisso!

M e i x o = r m ˙ ( V j - r ω ) ( 1 - cos ⁡ β )

Aqui m ˙ pode ser substituido por:

m ˙ = ρ V ˙

A potência de um eixo pode ser dada de uma forma geral por:

W ˙ e i x o = 2 π n ˙ M e i x o

Onde :

n ˙ = ω 2 π

Substituindo tudo chegamos nessa expressão aqui:

W ˙ e i x o = ω r ρ V ˙ ( V j - r ω ) ( 1 - cos ⁡ β )

Vamos comparar com o do enunciado?!!

W ˙ e i x o = ρ ω V ˙ ( V j - ω r ) ( 1 - cos ⁡ β )

Aweeee!!!!

Passo 2

Agora vamos para a segunda parte que é aplicar os valores do enunciado para a expressão que terminamos de achar!

W ˙ e i x o = ρ ω V ˙ ( V j - ω r ) ( 1 - cos ⁡ β )

Só relembrando...   ρ = 1000 k g m 3 ,   r = 2   m ,   V ˙ = 10 m 3 s ,   n ˙ = 150   r p m ,   β = 160 °   e   V j = 50 m s .

Opa, não temos ω , vamos calcular:

ω = 2 π n ˙

Substituindo:

ω = 2 π   150   r p m × 1   m i n 60   s

Já convertendo as unidades pra ficar tudo bonitinho

Agora partiu substituir tudo:

W ˙ e i x o = 1000 × 15,71 × 10 × 2 ( 50 - 2 × 15,71 ) ( 1 - cos ⁡ 160 ° ) = 11,3 × 10 6 W

Ou:

W ˙ e i x o = 11,3   M W

Resposta

W ˙ e i x o = 11,3   M W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de 2 kg é restringido horizontalmente, mas está livre para mover na direção vertical. O disco é atingido por baixo por um jato vertical de água. Na saída do bocal, a velocidade e o diâmetro d
Estudantes estão brincando com uma mangueira de água. Quando eles a apontam para cima, o jato de água atinge apenas uma das janelas do escritório do Professor Pritchard, a 10 m de altura. Se o diâmetr
4.82 Uma placa plana com um orifício de 50 mm de diâmetro está instalada na extremidade de um tubo de 100 mm de diâmetro. Água escoa através do tubo e do orifício com uma vazão de 0,57 m³/s. O diâmetr
4.81 Um dispositivo de formação de jato é mostrado no diagrama. A água é fornecida a p=10 kPa (manométrica) através da abertura flageada da água 1900 mm². A água sai do dispsitivo em um jato livre, em
4.80 Suponha que a curva do Problema 4.39 seja um segmento de um canal largo no plano horizontal. A pressão na entrada é de 170 kPa (abs) e na saída, 130 kPa (abs). Determine a força requerida para ma