Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 28
Mostre que, para qualquer canal prismático reto com escoamento uniforme, a tensão cisalhante média na parede é dada por:
Caso você já tenha deduzido esse resultado antes, use-o para resolver o P10.27.
Passo 1
Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Vamos fazer um desenho aqui rapidinho pra entender a parada!
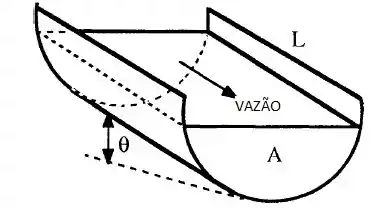
Passo 2
Fazendo um volume de controle em volta do fluido como mostrado na figura acima:
Mas por definição, os comprimentos se cancelam o que nos dará que
Resposta
Exercícios de Livros Relacionados
Água escoa de modo permanente em um canal retangular de 0,8m de largura a uma vazão de 0,7 m 3 / s . Se a profundidade do escoamento for 0,25m , determine a velocidade de escoamento e se o escoamento
Água a 15 ° C escoa a uma profundidade de 0,4m com velocidade média de 6m / s em um canal retangular Determine (a) a profundidade crítica, (b) a profundidade alternativa e (c) a energia mínima específ
Considere um canal de água com diâmetro interno de 1m feito de concreto polido ( n = 0,012 ) . A inclinação do canal é 0,002 . Para uma profundidade de escoamento de 0,25m no centro, determine a vazão
Um canal de água de ferro fundido em forma de V mostrado na Figura P13-55 tem uma inclinação do fundo de 0,5 ° . Para uma profundidade de escoamento de 1m no centro, determine a taxa de descarga no es
Repita o Problema 13-53 para um canal de terra escavado coberto de vegetação com n =0,030 .