Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 57
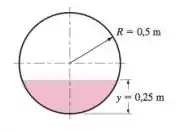
Considere um canal de água com diâmetro interno de feito de concreto polido A inclinação do canal é . Para uma profundidade de escoamento de no centro, determine a vazão da água através do canal.
Passo 1
Falaaaa aii!! Nessa questão nós temos um canal de água e queremos determinar a vazão da água através do canal, show? Vamos lá!
Passo 2
Temos que a área de fluxo da calota esférica é,
O perímetro é,
E o raio hidráulico é,
Passo 3
Então a vazão através do canal, usando a equação de Manning é,
Resposta
Exercícios de Livros Relacionados
Um canal trapezoidal com revestimento de tijolos tem uma inclinação do fundo de 0,001 e uma largura de base de 4 m, e as superfícies laterais tem ângulos de 30˚ da horizontal, como mostra a figura. Se
12-144 Ar entra em um duto adiabático de 4 cm de diâmetro a condições de entrada de M a 1=2,2 , T 1=250K e P 1=80k P a , e sai a um número de Mach de M a 2= 1,8 . Assumindo o fator médio de atrito de
12-149 Ar a condições sônicas, temperatura e pressão estáticas de 500Ke420k P a , respectivamente, deve ser acelerado até um número de Mach de 1,6 resfriando à medida que escoa através de um canal com
12-145 Ar é resfriado à medida que escoa através de um duto com 20 cm de diâmetro. As condições de entrada são M 1=1,2 , T 01 = 350K e P 1=240k P a e o número de Mach de saída é M a 2=2,0 . Desprezand
12-147 Repita o Problema 12-146 para o hélio.