Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 105

Um navio de 50 m de comprimento e 800 m2 de área molhada tem o formato de casco testado na Figura 7.19. Não há bulbos na proa nem na popa. A potência total de propulsão disponível é 1 MW. Para água do mar a 20°C, plote a velocidade do navio V em função da potência P para 0

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos um navio de comprimento L = 50   m e área molhada de A m = 800   m ² , com um propulsor que fornece uma potência de P = 1   M W .

O enunciado nos pede então pra traçar um gráfico da velocidade do navio V em função da potência do propulsor. Pra isso, vamos considerar a relação da potência com a força de arrasto F A , dada pela equação abaixo:

P = F A V

A força de arrasto será dada como uma contribuição da força de arrasto causada pelas ondas, F A , o n d a e a força de arrasto por atrito F A , o n d a , dadas pelas seguintes equações:

P = F A , o n d a + F A , o n d a V = ρ 2 C A , o n d a L 2 + C A , a t r   A m V ³

Nas condições dadas, vamos considerar as propriedades da água como sendo ρ = 998   k g / m ³ e μ = 1,0 × 10 - 3 P a ∙ s

No próximo passo eu vou te mostrar como calcular os coeficientes de arrasto dados nessa equação, então vem comigo pra gente resolver esse problema juntos!

Passo 2

Antes, vamos começar entendendo como proceder nesse problema.

Primeiro, vamos determinar valores de velocidade que serão utilizados pra calcular os coeficientes de arrasto. Depois, com os coeficientes de arrasto, iremos calcular os valores de potência correspondentes a essas velocidades utilizando a equação deduzida no Passo 1.

Pra calcular o coeficiente de arrasto dado pela ação das ondas, devemos ir no gráfico 7.19 na página 502, como na imagem abaixo:

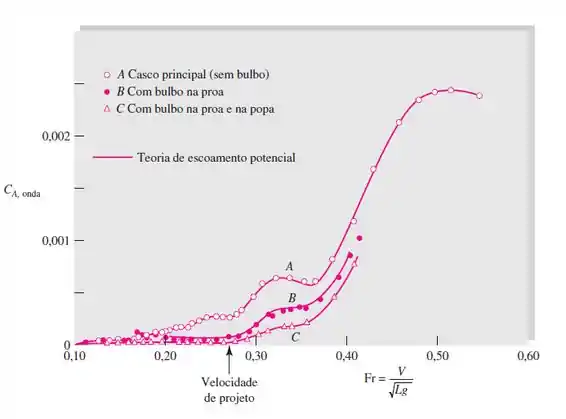
Devemos então entrar co o número de Froude F r , como dado na imagem, pra cada uma das velocidades determinadas.

Já para o coeficiente de arrasto pelo atrito será dado pela fórmula aplicada para o escoamento turbulento em uma placa plana, que é:

C A , a t r = 0,031 R e L 1 / 7 = 0,031 μ 1 / 7 ρ V L 1 / 7

Passo 3

Vamos variar a velocidade de 0 a 8 , 5   m / s , com passos de 1   m / s . Sendo assim, obtemos o seguinte gráfico de Velocidade por Potência:

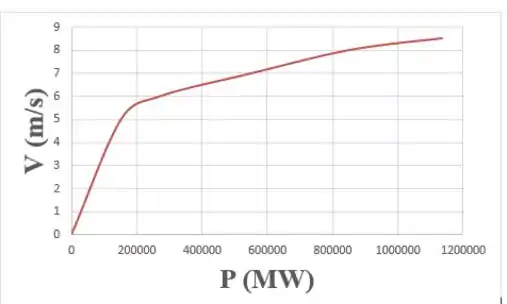
Como é possível ver pelo gráfico, um valor onde encontraríamos uma boa eficiência para a operação do navio é entre velocidades de 6   m / s e 7   m / s , onde podemos ver um grande aumento de potência para pequenos aumentos de velocidade.

Pronto, matamos a questão juntos!

Resposta

Um ponto de eficiência para a operação do navio é em velocidades entre 6   m / s e 7   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro longo de seção transversal retangular, com 5 cm de altura e 30 cm de comprimento, está imerso em água a 20°C escoando a 12 m/s paralelamente ao comprimento do retângulo. Calcule a força de
Uma rede de peixes consiste em fios de 1 mm de diâmetro sobrepostos e amarrados para formar quadrados de 1 cm por 1 cm. Calcule o arrasto de 1 m 2 de tal rede quando puxada normalmente ao seu plano a
Joe pode pedalar sua bicicleta a 10 m/s sobre uma pista plana quando não há vento. A resistência de rolagem de sua bicicleta é 0,80 N ⋅ s / m , isto é, 0,80 de força por m/s de velocidade. A área de a
Um veículo de entregas transporta um longo letreiro sobre o topo, como na Figura P7.56. Se o letreiro for muito fino e o veículo se mover a 105 km/h, (a) estime a força sobre o letreiro sem vento late
Da Tabela 7.2, o coeficiente de arrasto de uma placa larga ao escoamento é aproximadamente 2,0. As condições do escoamento são U ∞ e p ∞ . Se a pressão média sobre a parte frontal da placa for aproxim