Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 93

13-93 Considere um escoamento de água uniforme em um canal largo retangular com profundidade de 2 m e feito de concreto não polido com uma inclinação de 0,0022. Determine a vazão de escoamento da água por m de largura do canal. Agora a água escoa sobre uma saliência com 15 cm de altura. Se a superfície da água sobre a saliência permanecer plana (sem elevação ou queda), determine a variação da taxa de descarga da água por metro de largura do canal. Sugestão: Investigue se uma superfície plana sobre a saliência é fisicamente possível.

Passo 1

Bora pra mais um exercício!?

Aqui temos duas situações diferentes, então vamos pra primeira e depois a gente conversa sobre a segunda, beleza?!

Temos um canal aberto da seguinte forma:

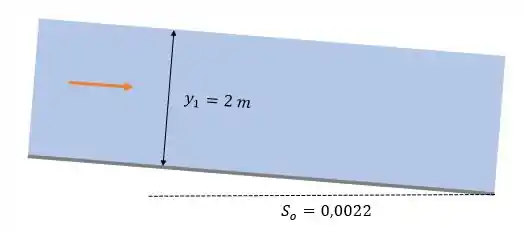
E queremos a vazão volumétrica por unidade de largura:

V ˙ b = a n A c R h 2 3 S o 1 2 1 b  

A área transversal é :

A c = y 1 × b = 2 b

O raio hidráulico, R h = y 1 = 2   m , lembrando que a = 1   m 1 3 / s e para o concreto polido n = 0,014 podemos achar:

V ˙ b = 1 0,014 × 2 b × 2 2 3 × 0,0022 1 2 1 b  

Calculando:

V ˙ b = 10,64   m 2 / s

Passo 2

Agora vamos pro segundo caso:

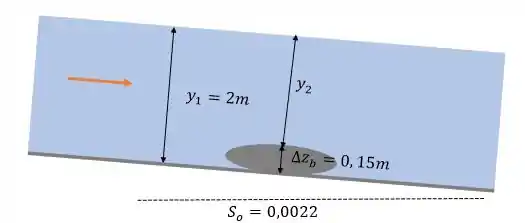
Dessa vez queremos encontrar a variação da taxa de descarga da água por metro de largura do canal:

E s 2 = E s 1 - Δ z b

Substituindo as energias específicas:

y 2 + V 2 2 2 g = y 1 + V 1 2 2 g - Δ z b

Mas:

y 2 = y 1 - Δ z b

Então ficamos com:

V 2 2 2 g = V 1 2 2 g

Cortando a gravidade:

V 1 = V 2

Opaaa, mas como assim as velocidades são iguais??!!! Vamos dar uma olhadinha na equação da continuidade:

y 2 V 2 = y 1 V 1

Mas y 1 ≠ y 2 , então as velocidades não podem ser iguais, certo?!

Logo não temos solução para essa situação, porque ela é fisicamente impossível!!

Resposta

V ˙ b = 10,64   m 2 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-81C Desenhe um diagrama de energia específica de profundidade para o escoamento das comportas submersas, e indique o escoamento através da comporta para os seguintes casos: (a) comporta sem atrito,
13-82C Como é definido o coeficiente de descarga C d das comportas basculantes? Quais são os valores normais deC d para as comportas basculantes com escoamento de saída livre? Qual é0 valor de C d par
13-79 Considere o escoamento da água em um canal com 10 m de largura a uma vazão de 70 mVs e uma profundidade de escoamento de 0,50 m. Agora a água sofre um salto hidráulico, ea profundidade de escoam
13-80 A profundidade do escoamento e a velocidade da água medidas após um salto hidráulico são 2 m e 3 m/s, respectivamente. Determine a profundidade e velocidade de escoamento antes do salto, e a fra
13-85C Considere o escoamento de um líquido sobre uma saliência durante o escoamento subcrítico em um canal aberto. A energia específica e a profundidade do escoamento diminuem sobre a saliência à med