Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 107

Nitrogênio líquido é armazenado em um vaso esférico com parede delgada, cujo diâmetro é de D i = 1   m . O vaso está posicionado concentricamente no interior de um recipiente esférico maior, também com parede delgada e que tem um diâmetro D e = 1,10   m . A cavidade formada entre os vasos esféricos é preenchida com hélio à pressão atmosférica.

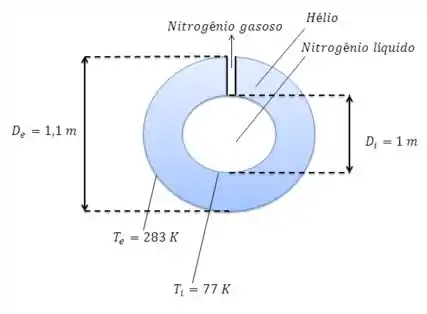
Sob condições normais de operação, as temperaturas nas superfícies das esferas interna e externa são T i = 77   K e T e = 283   K . Sendo o calor latente de vaporização do nitrogênio igual a - 3 × 10 5   J / k g , qual é a taxa mássica m ˙   ( k g / s ) de nitrogênio gasoso perdida no sistema?

Passo 1

Temos a seguinte situação: Dois vasos esféricos concêntricos de dimensões D i = 1   m e D e = 1,10   m possuem hélio no espaço entre eles. O vaso interno está armazenando nitrogênio líquido.

Como os dois vasos estão a temperaturas diferentes ( T i = 77   K e T e = 283   K ) haverá transferência de calor por convecção natural do gás hélio. Esta energia fornecida ao vaso interno será responsável por evaporar parte do nitrogênio líquido.

Sabendo que a entalpia de vaporização do nitrogênio é ∆ H e v = 3 × 10 5   J / k g devemos encontrar a taxa mássica de nitrogênio que evapora. Vamos lá?

Para começar vamos assumir que o processo ocorre em regime estacionário e que não há perdas de calor, ou seja:

q c o n v = q e v

4 π k e f 1 r i - 1 r e × T e - T i = m ˙ ∆ H e v

m ˙ = 4 π k e f 1 r i - 1 r e × T e - T i ∆ H e v

Já temos uma relação para obter a taxa mássica. Porém, para poder aplicá-la precisamos ainda determinar a condutividade térmica efetiva para este processo.

Passo 2

A primeira coisa a se fazer para determinar k e f é calcular a temperatura média do gás hélio no espaço entre os vasos. Ela é dada por:

T - m = T e + T i 2

T - m = 283 + 77 2

T - m = 180   K

Para esta temperatura as propriedades do hélio são (Tabela A-4, apêndice A):

ρ = 0,2708   k g / m 3

c p = 5193   J / k g K

ϑ = 51,3 × 10 - 6   m 2 / s

k = 107,2 × 10 - 3   W / m K

P r = 0,673

Antes de prosseguir vamos obter o comprimento característico para este sistema. Para um espaço esférico confinado:

L c = 1 r i - 1 r e 4 3 2 1 3 r i - 7 5 + r e - 7 5 5 3

L c = 1 0,5 - 1 0,55 4 3 2 1 3 ( 0,5 ) - 7 5 + 0,55 - 7 5 5 3

L c = 5,689 × 10 - 3   m

Passo 3

Agora que temos o comprimento característico e as propriedades do fluido podemos calcular o número de Rayleigh:

R a e = g β ∆ T L c 3 k ρ c p × ϑ

R a e = 9,81 × 1 T - m × ( T e - T i ) × 5,689 × 10 - 3 3 107,2 × 10 - 3 0,2708 × 5193 × 51,3 × 10 - 6

R a e = 9,81 × 1 180 × ( 283 - 77 ) × 5,689 × 10 - 3 3 107,2 × 10 - 3 0,2708 × 5193 × 51,3 × 10 - 6

R a e = 528,7

Podemos agora obter a condutividade térmica efetiva através da correlação:

k e f = 0,74 × k × P r 0,861 + P r 1 4 × R a e 1 4

k e f = 0,74 × 107,2 × 10 - 3 × 0,673 0,861 + 0,673 1 4 × 528,7 1 4

k e f = 0,31   W / m K

Por fim, vamos aplicar a nossa relação para a taxa mássica de evaporação de nitrogênio:

m ˙ = 4 π k e f 1 r i - 1 r e × T e - T i ∆ H e v

m ˙ = 4 × π × 0,31 1 0,5 - 1 0,55 × 283 - 77 3 × 10 5

m ˙ = 0,015   k g / s

Resposta

A taxa mássica de evaporação será m ˙ = 0,015   k g / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere as condições do Problema 9.19, só que agora há uma diferença entre as temperaturas superficiais interna e externa da janela, T s , i e T s , e . Para uma espessura e condutividade térmica do
Uma placa de alumínio quadrada, com 5m m de espessura e 200m m de lado, é aquecida enquanto permanece suspensa, em posição vertical, em ar quiescente a 40 ° C . Determine o coeficiente de transferênci
Um objeto sólido deve ser resfriado pela sua submersão em um fluido quiescente. O coeficiente de transferência de calor associado ao processo de convecção natural é dado por h - =C Δ T 1 4 , sendo C u
Durante um dia de inverno, a porta de vidro de uma porta balcão externa, com altura de 1,8 m e largura de 1,0m , mostra uma linha de gelo próximo a sua base. A temperatura das paredes da sala e do ar
Determine o coeficiente de transferência de calor médio nas paredes verticais, com 2,5m de altura, de uma casa na qual o ar interior e a temperatura superficial das paredes são, respectivamente, ( a )