Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 101

Um projeto de coletor solar é constituído por um tubo interno inserido concentricamente em um tubo externo, que é transparente à radiação solar. Os tubos têm paredes delgadas e os diâmetros dos tubos interno e externo são de 0,10   m e 0,15   m , respectivamente. O espaço anular entre os tubos é completamente fechado nas extremidades e preenchido por ar à pressão atmosférica. Sob condições de operação, nas quais as temperaturas nas superfícies dos tubos interno e externo são de 70 ° C e 30 ° C , respectivamente, qual é a perda de calor por convecção através da camada de ar, por metro de comprimento do tubo?

Passo 1

Vamos começar esquematizando a nossa situação:

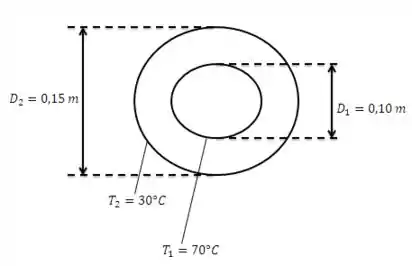
Temos um duto cilíndrico de diâmetro D 1 = 0,10   m revestido por uma camada de diâmetro D 2 = 0,15   m preenchida com ar. Sabendo que as temperaturas da superfície interna e externa são T 1 = 70 ° C e T 2 = 30 ° C , respectivamente, devemos calcular a taxa de transferência de calor por convecção na camada de ar.

Para isso, vamos começar calculando a temperatura média do ar. Ela é dada por:

T - m = T 1 + T 2 2

T - m = 70 + 30 2

T - m = 50 ° C = 323   K

Nesta temperatura, as propriedades do ar são (Tabela A-4, apêndice A):

ρ = 1,0849   k g / m 3

c p = 1007,9   J / k g K

ϑ = 18,20 × 10 - 6   m 2 / s

k = 28 × 10 - 3   W / m K

P r = 0,704

Passo 2

Agora que encontramos as propriedades do ar nosso próximo passo será calcular o comprimento característico:

L c = 2 ln ⁡ r 2 r 1 4 3 r 1 - 3 5 + r 2 - 3 5 5 3

L c = 2 × ln ⁡ 0,075 0,05 4 3 0,05 - 3 5 + 0,075 - 3 5 5 3

L c = 1,144 × 10 - 2   m

A partir deste valor podemos determinar o número de Rayleigh para este processo:

R a c = g β ∆ T L c 3 k ρ c p × ϑ

R a c = 9,81 × 1 T - m × ( T 1 - T 2 ) × 1,144 × 10 - 2 3 28 × 10 - 3 1,0849 × 1007,9 × 18,20 × 10 - 6

R a c = 9,81 × 1 323 × ( 70 - 30 ) × 1,144 × 10 - 2 3 28 × 10 - 3 1,0849 × 1007,9 × 18,20 × 10 - 6

R a c = 3898,3

Passo 3

O próximo passo para chegarmos à transferência de calor por convecção natural é obter a condutividade térmica efetiva. Para um cilindro, ela é dada pela relação:

k e f k = 0,386 × P r 0,861 + P r 1 4 × R a c 1 4

k e f = k × 0,386 × P r 0,861 + P r 1 4 × R a c 1 4

k e f = 28 × 10 - 3 × 0,386 × 0,704 0,861 + 0,704 1 4 × 3898,3 1 4

k e f = 69,94 × 10 - 3   W / m K

Por fim, vamos aplicar a equação de taxa de transferência de calor por unidade de comprimento de tubo para um espaço fechado cilíndrico:

q ' = 2 π k e f ln ⁡ D 2 D 1 T 1 - T 2

q ' = 2 × π × 69,94 × 10 - 3 ln ⁡ 0,15 0,1 70 - 30

q ' = 43,4   W / m

Resposta

A perda de calor por comprimento da tubulação é q ' = 43,4   W / m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Certos projetos de fornos que queimam madeira se baseiam exclusivamente na transferência de calor por radiação e convecção natural para a vizinhança. Considere um forno que forma um compartimento cúbi
Placas de circuitos integrados (CI) são colocadas no interior de um duto e dissipam um total de 500 W. O duto tem uma seção transversal quadrada com w = H = 150 mm e um comprimento de 0,5 m. O ar entr
Uma longa linha de vapor não isolada, na posição horizontal, com 89 mm de diâmetro externo e uma emissividade de 0,8, transporta vapor a 200°C e está exposta ao ar atmosférico e a uma grande vizinhanç
Como está evidente nos dados de propriedades nas Tabelas A.3 e A.4, a condutividade térmica do vidro na temperatura ambiente é mais do que 50 vezes maior do que a do ar. Consequentemente, é desejável
Para reduzir perdas térmicas, um duto retangular horizontal, com W = 0,8 m de largura e H = 0,3 m de altura, encontra-se envolto por uma barreira de radiação. A parede do duto e a barreira estão separ