Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 89
Uma companhia de seguros contratou você como consultor para melhorar a sua compreensão a respeito de queimaduras. Eles estão especialmente interessados em queimaduras causadas pelo contato de parte do corpo do trabalhador com máquinas que se encontram a temperaturas elevadas, na faixa de 50 a 100 °C. O consultor médico da companhia informa que ferimentos térmicos irreversíveis (morte das células) irão ocorrer se qualquer tecido vivo for mantido a T ≥ 48 °C por um intervalo Δt ≥ 10 s. Eles desejam informações no que diz respeito ao grau de extensão dos danos irreversíveis ao tecido celular (medido pela distância da superfície da pele) em função da temperatura da máquina e do tempo de contato entre a pele e a máquina. Considere que células vivas têm uma temperatura normal de 37 °C, sejam isotrópicas e tenham propriedades constantes equivalentes às da água líquida.
(a) Para avaliar a seriedade do problema, calcule as posições no tecido celular onde a temperatura atingirá 48 °C após 10 s de contato com máquinas a 50 °C e a 100 °C.
(b) Para uma temperatura da máquina de 100 °C e 0 ≤ t ≤ 30 s, calcule e represente graficamente os históricos das temperaturas no tecido a 0,5; 1 e 2 mm da superfície da pele.
Passo 1
Beleza! Nesse exercício, vamos modelar o problema como sendo um sólido semi-infinito com temperatura na superfície constante, então a temperatura em um ponto, para um determinado intervalo de tempo, pode ser encontrada a partir da equação 5.60, que é dada por:
Então, avaliando os dois casos propostos na letra (a), para temperatura das máquinas a 50 °C e 100 °C, o lado esquerdo dessa equação será:
Agora nós vamos recorrer à tabela A.6 do apêndice A para encontrar as propriedades da água na temperatura de 37 °C = 310 K, então, teremos:
E, com esses valores, podemos calcular o valor de , que será:
Passo 2
Então, analisando primeiro para o caso onde temos , a equação do passo 1 se torna:
Então, agora precisamos recorrer à tabela B.2 do apêndice B para encontrar o valor da função erro de Gauss, com isso, a nossa equação se torna:
Agora, da mesma forma, para , temos:
Então, agora precisamos recorrer à tabela B.2 do apêndice B para encontrar o valor da função erro de Gauss, com isso, a nossa equação se torna:
Passo 3
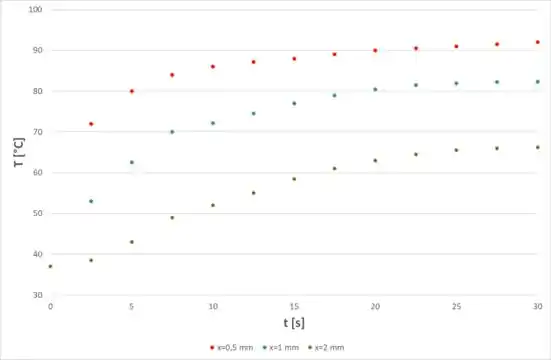
Agora, para a letra (b), nós vamos utilizar a temperatura da máquina sempre a 100 °C, analisando as temperatuas nos níveis 0,5; 1 e 2 mm para o intervalo de tempo de 0 até 30 segundos. Vamos fazer essa análise utilizando a mesma equação utilizada nos passos 1 e 2, só que agora deixaremos ela em função do tempo, então, teremos:
Então, repetindo os cálculos para os diferentes valores de e deixando em função do tempo, conseguimos obter o seguinte gráfico:
