Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 134
Observando na Figura 13.16 que a emissividade de gases pode ser aumentada pela adição de vapor de água, é proposto aumentar a transferência de calor com a injeção de vapor de água saturado a 100°C na entrada do tubo do Problema 13.133. A vazão mássica injetada de vapor é
50% da vazão mássica de vapor de água nos produtos da combustão. Determine a radiação do gás para a parede do tubo com e sem a injeção do vapor de água. Sugestão: A temperatura dos gases quentes diminui e as pressões parciais do vapor de água e do CO2 mudam quando vapor, relativamente frio, é injetado. Use seu conhecimento de misturas gasosas da termodinâmica para calcular as pressões parciais e as vazões mássicas. Suponha que a massa molar da mistura original seja igual a do ar.
Passo 1
É isso ai galerinhaaa !! Vamos continuando?
Bom, a questão nos pediu para calcular a radiação do gás para a parede do tubo com e sem a injeção do vapor de água, certo?
No problema anterior nós já calculamos a radiação para a parede quando não há injeção de vapor!
Vamos relembrar?
O problema anterior já nos disse que:
Então:
Quando nós adicionamos o vapor nós vamos usar a mesma fórmula, mas e serão diferentes !!
Passo 2
Para isso nós precisamos fazer um novo balanço energético para os produtos de combustão e o vapor injetado!
No caso da temperatura:
Nós sabemos que:
Ainda não temos nem , mas sabemos que a vazão mássica da saída é a soma da vazão inicial e do novo vapor adicionado:
Então, a única coisa que precisamos achar é !!
Inicialmente nós tínhamos um caudal mássico de vapor de água igual a , como o problema nos disse que foi adicionado 50% do caudal mássico inicial:
Onde é a fração mássica de vapor de água, e pode ser calculado como:
Lembrando dos dados que precisamos:
E substituindo:
Na temperatura:
E substituindo:
Passo 3
Agora nós temos que achar !!
Para conseguir achar nós vamos ter que começar achando a nova pressão parcial para cada gás, dióxido de carbono e vapor de água!
Bom, a nova fração parcial é dada por:
A nova fração parcial da água é dada por:
Lembrando que:
Então:
E para o dióxido de carbono:
Para achar a emissividade do vamos dar uma olhada nesta figura aqui:
E para o vapor de água esta:
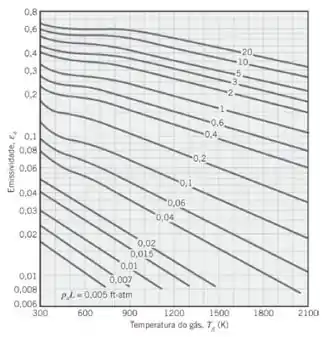
Para cilindros:
Mas o gráfico nos pediu em transformando:
Interceptando no gráfico, quando
Mas o que nós queremos aqui é !!
E para isso nós vamos usar uma formulinha:
Para achar nós vamos precisar de mais um gráfico:
Calculando o que ainda não temos:
No último gráfico:
Ufaaaa !! Agora sim:
E agora é só colocarmos na fórmula que já vimos no Passo 1:
E é isso aí galerinha !! Mais uma vencida com sucesso !!