Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 135

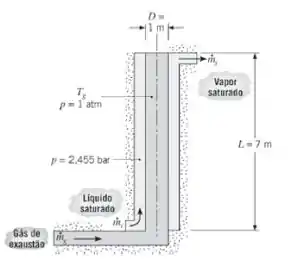
A recuperação de calor dos gases de exaustão de um forno de fundição é feita com a passagem dos gases através de um tubo metálico vertical e a introdução de água saturada (estado líquido) na parte inferior de uma região anular ao redor do tubo. O comprimento do tubo e seu diâmetro interno são de 7 e 1 m, respectivamente, e a superfície interna do tubo é negra. O gás no interior do tubo encontra-se à pressão atmosférica, com pressões parciais de CO2 e

de H2O (vapor) iguais a 0,1 e 0,2 atm, respectivamente, e sua temperatura média pode ser aproximada por T g   =   1400   K . A vazão do gás é de   m g ˙ =   2   k g / s . Se água saturada for alimentada a uma pressão de 2,455 bar, estime a vazão de água m s ˙ para a qual há conversão completa de líquido saturado na alimentação para vapor saturado na saída. As propriedades termofísicas do gás podem ser aproximadas por μ   =   530   × 10 - 7 k g s m ,   k   =   0,091 W m K e   P r   =   0,70 .

Passo 1

É isso ai galerinhaaa !! Vamos continuando?

Bom, a questão nos pediu apenas a vazão de água m s ˙ para a qual há conversão completa de líquido saturado na alimentação para vapor saturado na saída, ok?

Para que o líquido passe para vapor nós devemos fornecer calor, não é? E esse calor nós já sabemos como calcular:

q = m s ˙ h f g

Como o fluido está recebendo calor por convecção e radiação:

q = A s [ E g - α g σ T s 4 ] + h - A s T g - T s

A irradiação pode ser reescrita como:

E g = ε g σ T g 4

Então:

q = A s [ ε g σ T g 4 - α g σ T s 4 ] + h - A s T g - T s

Lembrando que:

A s = π D L

Como o que nós estamos procurando é o q , vamos só isolá-lo:

q = π D L ε g σ T g 4 - α g σ T s 4 + h - T g - T s

Substituindo:

m s ˙ = π D L ε g σ T g 4 - α g σ T s 4 + h - T g - T s h f g

Shoooow !!

Agora vamos ver o que já temos?

σ = 5,64 × 10 - 8 W m 2 K 4

T g = 1400   K

T s = 400   K

D = 1   m

L = 7 m

E tabelado nós temos:

h f g = 2183 × 10 3 J k g

Então nós só precisamos achar ε g , α g e h - !!

Passo 2

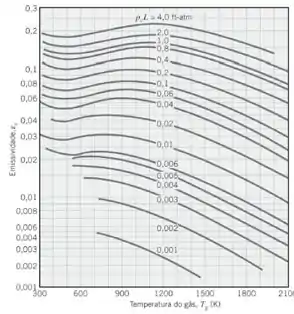
Para achar a emissividade do gás vamos dar uma olhada nesta figura aqui:

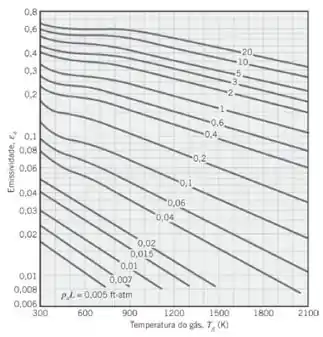
E para a água esta:

Para o cilindro:

p a L = 0 , 2 0   a t m 0,95 D = 0 , 2   a t m 0,95 × 1 m = 0 , 2   a t m 0,95   m

p c L = 0 , 1   a t m 0,95 D = 0 , 1   a t m 0,95 × 1   m = 0 , 1   a t m 0,95   m

Mas o gráfico nos pediu em f t . a t m ,   transformando:

p a L = 0 , 2   a t m 0,95   m × 3,28   f t 1   m = 0 , 623   f t . a t m

p c L = 0,1   a t m 0,95   m × 3,28   f t 1   m = 0,312   f t . a t m

Interceptando no gráfico, quando T g = 1400   K :

ε a = 0 , 1 3

ε c = 0,0 95

Mas o que nós queremos aqui é ε g !!

E para isso nós vamos usar uma formulinha:

ε g = ε a + ε c - ∆ ε

Para achar ∆ ε nós vamos precisar de mais um gráfico:

Calculando o que ainda não temos:

P a P c + P a = 0 , 2   a t m 0,1   a t m + 0 , 2   a t m = 0,67  

L P c + P a = 0,95 × 1 m × 3,28   f t 1   m 0,10   a t m + 0 , 2   a t m = 0 , 935   f t . a t m

No último gráfico:

∆ ε = 0,036

Ufaaaa !! Agora sim:

ε g = 0 , 1 3 + 0,0 95 - 0,0 36 = 0,1 89

Passo 3

Para a absortividade nós temos uma fórmula para o vapor de água e para o gás!

α a = T g T s 0,45 ε a T s ,   p a L T s T g

α c = T g T s 0,6 5 ε c T s ,   p c L T s T g

Substituindo:

α a = 1400 400 0,45 ε a 400   K ,   0,623     f t . a t m 400 1400

α a = 1400 400 0,4 5 ε a 400   K ,   0,1 78   f t . a t m

No gráfico apresentado no Passo 2 para o vapor de água:

α a = 1400 400 0,45 0,1 4 = 0 , 24 6

Para o dióxido de carbono:

α c = 1400 400 0 , 6 5 ε c 400   K ,   0,312     f t . a t m 400 1400

α c = 1400 400 0,6 5 ε c 400   K ,   0,0 89   f t . a t m

No gráfico apresentado no Passo 2 para o vapor de água:

α c = 1400 400 0,6 5 0,0 67 = 0 , 151

Mas o que nós queremos aqui é α g !!

E para isso nós vamos usar uma formulinha:

α g = α a + α c - ∆ α

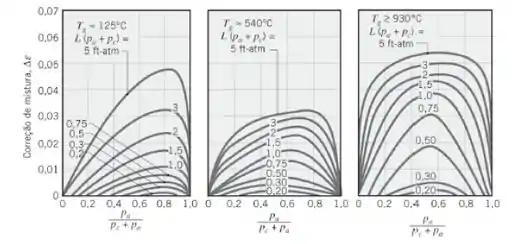
Podemos calcular ∆ α usando novamente a figura do Passo 2:

Usando os valores que já calculamos:

P a P c + P a = 0,67  

L P c + P a = 0 , 935   f t . a t m

Como a temperatura é próxima de 125°C na superfície:

∆ α ≅ 0,0 3 6

Então:

α g = 0 , 24 6 + 0 , 151 - 0,0 63 = 0,361

Passo 4

Shooow de bolinhas !!

Agora só precisamos do coeficiente convectivo, e para isso precisamos do famoso Reynolds:

R e D = 4 m g ˙ π D μ

Já sabemos que:

μ   =   530   × 10 - 7 k g s m

k   =   0,091 W m K

P r   =   0,70

m g ˙ = 2 k g s

Então:

R e D = 4 1 π 1 530 × 10 - 7 ≅ 48047

Como o fluxo é turbulento nós podemos usar a correlação de Dittus – Boelter:

h - = k D 0,023 R e D 4 5 P r 0,3

Substituindo:

h - = 0 , 091 1 0,023 48047 4 5 0 , 70 0,3 = 10,5 W m 2 K

Eita lasqueira !!! Esta é grande ein !! Mas agora nós vamos substituir na fórmula que achamos no Passo 1 e prontinhoo:

m s ˙ = π 1 7 0,189 5,87 × 10 - 8 1400 4 - 0,361 5,87 × 10 - 8 400 4 + 10,5 1400 - 400 2183 × 10 3

m s ˙ = 0,515 k g s

Shoooow !! Chegamos ao fim de mais umaa !!

Resposta

m s ˙ = 0,515 k g s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

104 - Um grande número de longos tubos, cada um com diâmetro D , é colocado paralelo um ao outro e com distância centro a centro s .Uma vez que todos os tubos são geometricamente semelhantes e estão n
113 - Dois discos paralelos concêntricos, 20c m e 40c m de diâmetro são separados por uma distância de 10c m .O disco menor ( ε = 0,80 ) se encontra a uma temperatura de 300° C .O disco maior ε = 0,60
Considere um forno hemisférico com uma base circular plana de diâmetro D. Determine o fator de forma da cúpula desse forno até sua base.
Três cilindros paralelos infinitamente longos, de diâmetro D, estão localizados a uma distância s um do outro. Determine o fator forma entre o cilindro do meio e o do entorno.
Considere uma superfície cilíndrica e um disco orientado coaxialmente, como mostrado na Fig. 13-19. O cilindro tem um diâmetro D e um comprimento L. O disco de diâmetro D é colocado coaxialmente com o