Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 116
An observer at sea level does not hear an aircraft flying at
12,000-ft standard altitude until it is 5 (statute) mi past her.
Estimate the aircraft speed in ft/s.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Os dados são os seguintes:
Altitude da aeronave,
A distância axial após o observador, 5 milhas
A figura mostrando a posição da aeronave e o observador é a seguinte
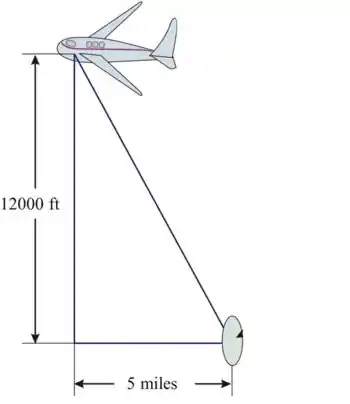
Passo 2
Da figura acima,
Daqui
Passo 3
Da relação entre o número de Mach e , temos
Agora, a partir da Tabela de Propriedades da atmosfera padrão, a dada altitude de ), a temperatura é aproximadamente
Da Tabela de Propriedades da atmosfera padrão, a zero altitude, a temperatura é A média dastemperaturas nessas altitudes é
Passo 4
Da tabela de propriedades dos gases
Relação de calor específica do ar, Constante de gás do ar,
Na temperatura média, a velocidade do som é
Agora a velocidade do avião é
Portanto, a velocidade das aeronaves é