Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 87
A vane turns a water jet through an angle α, as shown in
Fig. P3.87. Neglect friction on the vane walls. (a) What is
the angle α for the support force to be in pure compression?
(b) Calculate this compression force if the water velocity is
22 ft/s and the jet cross section is 4 in2.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
a) desenhando o diagrama de corpo livre de todas as forças agindo no volume de controle
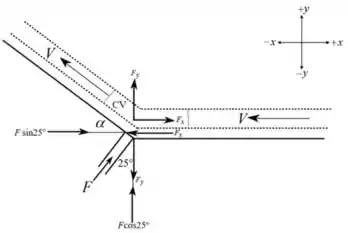
Passo 2
Escreva uma expressão para a força de direção que atua no volume de controle.
Portanto, quando então é positivo, significa que agirá na direção positiva de Escreva uma expressão para a força do componente que atua no volume de controle.
A força igual e oposta atuará em e na direção, respectivamente, na palheta pela terceira lei do movimento de Newton.
Passo 3
Agora aplique a equação de equilíbrio de força para a palheta na direção .
Aplique a equação de equilíbrio de força para a palheta na direção .
Passo 4
Substitua o valor de na equação (1),
Portanto, o ângulo para a força de suporte estar em compressão pura será .
Passo 5
b) Calcular a força de compressão a partir da equação (2),
Portanto, a força de compressão será .
Resposta
a)
b)