Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 18

A fim de determinar a viscosidade de um líquido de densidade de 0,95, você preenche, a uma profundidade de 12 cm, um grande recipiente com drenagem por um tubo vertical de 30 cm de comprimento fixado ao fundo. O diâmetro do tubo é 2 mm, e a taxa de drenagem é 1,9 cm³/s. Qual é o valor da viscosidade do fluido? O escoamento no tubo é laminar?

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Bora antes desenhar pra gente conseguir entender as paradas?

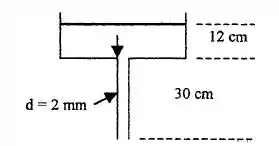
Bem, como conhecemos a vazão de escoamento e a área de escoamento é moleza a gente encontrar a velocidade de escoamentoooo!!!

Q = 1,9 c m 3 s = 1,9   x   10 - 6 m 3 s

V = Q A = Q π 4 d 2 = 1,9   x   10 - 6 π 4 0,002 2 = 0,605   m / s

Passo 2

O enunciado disse pra gente que o líquido tem d = 0,95, ou seja, sua densidade deve ser dada como sendo ρ l í q u i d o = 0,95   ρ á g u a = 0,95   998 = 948   k g / m ³

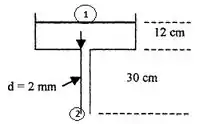
Escrevendo a equação de energia entre a superfície superior e saída do tubo, temos:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 g + z 2 + h f

Passo 3

Temos as pressões iguais no ponto 1 e no ponto 2, afinal estão ambas abertas à atmosfera. No topo do nosso paranauê aí, o fluido pode ser considerado estagnado, ou seja, V 1 ≈ 0 .

z 1 = V 2 2 2 g + h f

Bem, vamos estimar inicialmente que temos um escoamento laminar para abrirmos o valor de h f como sendo:

z 1 = V 2 2 2 g + 32 μ L V ρ g d 2

Importante notar que no nosso caso, V 2 = V , uma vez que a velocidade no ponto 2 é exatamente a velocidade que estava dentro do tubo na iminência do fluido ao sair do tubo. L é o tamanho do nosso tubo, beleza? E Z 1 é a altura entre o ponto 1 e 2.

0,42 = 0,605 2 2   x   9,81 + 32 μ 0,3 0,605 948 9,81 0,002 2 → μ = 0,00257 k g m . s  

Passo 4

Beleza, teoricamente encontramos nosso resultado! Mas precisamos antes verificar se nossa hipótese de escoamento laminar foi válida ou não. Bem, com a velocidade e viscosidade que encontramos, vamos verificar o valor de Re.

R e = ρ V d μ = 948 0,605 0,002 0,00257 = 446   L a m i n a r

Resposta

μ = 0,00257 k g m . s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor elétrico fornece 3 kW à bomba da instalação da figura, que tem um rendimento de 80%. Sendo dados:a) as tubulações são de mesma seção, cujo diâmetro é de 5 cm e de mesmo material;b) k s 1 = 10
Numa certa região, há três reservatórios naturais, A, B e C, e um conjunto TB formado por uma turbina acoplada diretamente a uma bomba. As perdas de carga nas tubulações são:Entre a e b, H p a , b = 0
Calcular a vazão na tubulação da figura para H = 10m . Calcular em seguida o novo valor de H para que a vazão seja 50L / s . Dados: D = 150m m ;ν = 1,05.10 - 6m 2 / s ; γ = 10 4N / m 3 ; k = 25,9.10 -
SAE 30 oil at 208C fl ows at 1.8 ft3/s from a reservoir into a6-in-diameter pipe. Use fl at-plate theory to estimate theposition x where the pipe wall boundary layers meet in thecenter. Compare with E
Etilenoglicol escoa com uma vazão de 0,01 kg/s através de um tubo com parede delgada e diâmetro de 3 mm. O tubo, em forma de serpentina, encontra-se submerso em um banho agitado de água que é mantido