Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 15
O professor Gordon Holloway e seus alunos na Universidade de New Brunswick foram a uma lanchonete e tentaram tomar milkshakes de chocolate ( por meio de canudos roliços de 8 mm de diâmetro e 30 cm de comprimento. (a) Verifique que seus pulmões humanos, os quais podem desenvolver pressões vacuométricas em torno de 3000 Pa, não seriam capazes de aspirar o milkshake pelo caminho vertical. (b) Um aluno cortou 15 cm do seu canudo e passou a tomar o milkshake alegremente. Qual é a vazão de fluido produzida por essa estratégia?
Passo 1
E aí, gente!! Tudo bem? Nesse exercício quero te mostrar que mais importante do que sabermos fazer conta, é interpretamos resultados algébricos, onde eles muitas vezes já nos dão respostas claras do que precisamos tomar como decisão!!
Bem, vamos escrever a nossa equação de energia:
Vamos considerar nosso canudo da seguinte maneira!
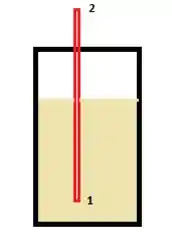
Ali embaixo o fluido pode ser considerado basicamente parado, então sua velocidade é zero, assim como também nosso ponto . E quanto a pressão? Bem, pro fluido subir, o vácuo formado dentro da boca da gente deve ter um valor em módulo muito maior do que a pressão no ponto 1 para que o fluido suba, certo? Então podemos escrever que .
Passo 2
(a) Note que o problema pede pra gente testar o que acontece quando nossos pulmões fazem uma pressão vacuométrica em torno de 3000 Pa!! Mas lembra-se, estamos falando de pressões negativas pois estamos falando de vácuo!!
Note que de cara já vemos que isso dará negativo, pois a continha e como a velocidade é positiva, assim como a gravidade (escalar), vamos ter que
Isso é IMPOSSÍVEL!!!!
Passo 3
Mas né, pelamor de God!! Quem usa um canudo de 30 cm pra poder beber um milkshake!!!!!! Vamos cotar esse treco aí na metade e assumir que teremos um escoamento laminar, beleza?
Para escoamentos laminares, podemos aproximar nossa perda de carga pela aproximação de Poiseuille para escoamentos laminares dentro de tubos cilíndricos!!
Note que teremos uma equação quadrática tal que:
Vamos ter duas raízes para esse trem aí, e uma delas será negativa, ou seja, não liga pra ela e pega só a raiz positiva!!
Passo 4
Acabouuuuuu!!!!??? NÃOOOOOOOOOOOOO!!!
Como assumimos escoamento laminar, a gente agora tem que comprovar que nossa hipótese foi válida!
Show, realmente nosso escoamento era laminar!!!