Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 93
Um óleo de motor a 40°C está escoando sobre uma longa placa plana com velocidade de 4 m/s. Determine a distância xcr a partir do bordo de ataque da placa plana onde o escoamento se torna turbulento, calcule e faça um gráfico da espessura da camada limite sobre um comprimento de 2xcr.
Passo 1
Fala aí, tudo bem? Vem comigo que eu vou te ajudar a interpretar o enunciado e resolver esse problema.
Nessa questão, a gente tem uma placa plana de onde ocorre um escoamento de óleo de motor a .
A gente quer, então, calcular a espessura da camada limite em cada ponto da placa. Pra isso, a gente vai utilizar as seguintes equações, respectivamente para os fluxos Laminar e Turbulento:
Onde o número de Reynolds, que pode ser calculado a partir da equação:
Sendo a velocidade do escoamento, a viscosidade cinemática do fluido e o ponto da placa que estamos analisando.
A gente tem que calcular essas espessuras pra uma placa de comprimento , sendo o comprimento da placa a partir do qual o escoamento se torna turbulento, que corresponde a um valor de Reynolds de .
MAS PERA UM POUCO! Antes da gente ir pro próximo passo, a gente tem que buscar a viscosidade cinemáticas pro óleo de motor a na Tabela A-7 (página 777):
Pronto! Agora sim, vem comigo que nos próximos passos a gente vai resolver essa questão!
Passo 2
Vamo começar então. A gente vai começar calculando o comprimento pro qual o escoamento começa a ficar a turbulento.
Dessa forma:
Ou seja, vamos calcular os valores da espessura da camada limite pra uma placa de .
Vamos calcular então as espessuras da camada limite ao longo da placa em intervalos de .
Agora a gente tem que checar, a partir do número de Reynolds, se o fluxo é laminar ou turbulento.
Primeiro, vamo começar calculando pra um valor onde o escoamento é laminar, sendo . Calculando o número de Reynolds, temos:
Confirmado com o número de Reynolds que o escoamento é laminar, a gente usa a equação pra camada limite laminar:
Agora, vamo começar calcular um valor de onde o escoamento é turbulento, sendo . Calculando o número de Reynolds, temos:
Confirmado com o número de Reynolds que o escoamento é turnulento, a gente usa a equação pra camada limite turbulenta:
E a gente vai repetir isso até chegarmos ao comprimento todo da placa, com : primeiro calculamos o número de Reynolds, checamos se é laminar ou turbulento, aplicamos a equação correta pra e calculamos a espessura.
Como é uma mera repetição de passos, vou resumir essas respostas na tabela abaixo:
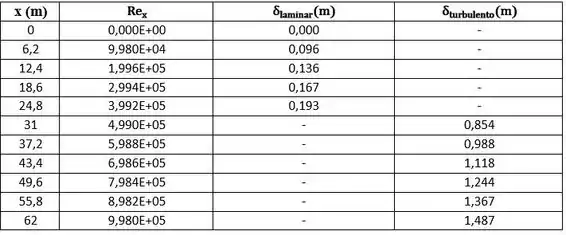
Pra finalizar a questão, vamos agora traçar um gráfico no Excel da espessura da camada limite ao longo da placa pros valores que calculamos:
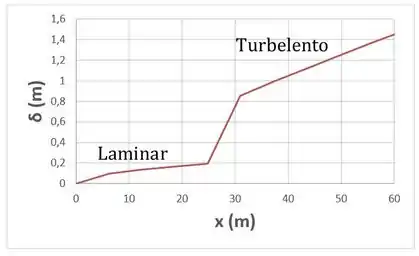
Agora terminamos a questão juntos!
Resposta
O gráfico das espessuras das camadas limite laminares e turbulentas sobre a placa plana de é:
