Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 93

Seja o Problema 7.113 . Estime a taxa de transferência de calor para o ar, levando em conta o aumento da temperatura do ar ao longo de seu escoamento através da espuma e a resistência térmica associada à condução na espuma na direção x . Você espera que a taxa de transferência de calor real para o ar seja igual, menor ou maior do que o valor que você calculou?

Passo 1

Vamos lá!!

O problema é relativamente simples temos ar que escoa através de uma espuma de cobre com temperaturas de superfície inferior e superior T s = 80 ° C .

Nosso problema nos pede a taxa de calor com a temperatura variando ao longo do eixo x .

Mas agora vamos ilustrar isso com nosso esqueminha pra facilitar.

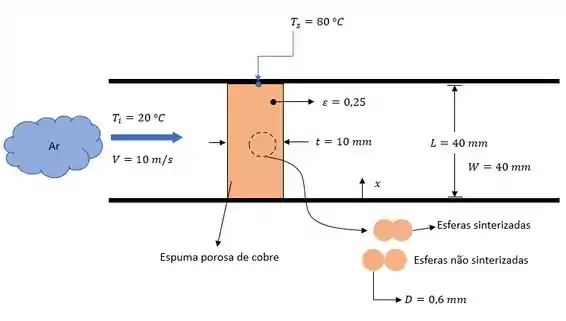
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - R e g i m e   p e r m a n e n t e

I I I - O   c o e f i c i e n t e   d e   t r a n s f e r ê n c i a   d e   c a l o r   p o d e   s e r   c a l c u l a d o   v i a   a n a l i s e   d e   l e i t o

I V - A   e s p u m a   s e   c o m p o r t a   c o m o   u m a   s u p e r f i c i e   e s t e n d i d a

V - E f i c i ê n c i a   t é r m i c a   c o n d u t i v a   p o d e   s e r   c a l c u l a d a   d a   r e l a ç ã o   d e   M a x w e l l

V I - T r o c a   d e   c a l o r   p o r   r a d i a ç ã o   d e s p r e z í v e l

Passo 2

Vamos lá! Usaremos os dados para o cobre comercial encontrados na tabela A - 1 e para o ar encontrados na tabela A - 4 , ambos à T = 325 K .

Seguindo a lógica do exemplo 11.7 sendo nossa espuma simétrica termicamente vamos usar a consideração I I I para encontrarmos nosso coeficiente, da equação 7.81 temos:

ε j - H = ε ⋅ h - ρ c p V P r 2 3 = 2,06 R e - 0,575

Sendo R e = 10   m s ⋅ 0,00006   m 18,41 ⋅ 10 - 6   m 2 s = 326

h - = ρ ⋅ c p ⋅ V ⋅ 2,06 R e - 0,575 P r 2 3 = 2,06 ⋅ 1,0782 ⋅ 10 ⋅ 326 - 0,575 0,704 2 3

h - = 4.060   W m 2 ⋅ K

Agora vamos calcular a área de superfície das partículas sinterizadas, sendo N o número de partículas temos:

A p ,   t = N π D 2 = 6 1 - ε W t L D

0,12   m 2

Agora se pegarmos um pedacinho d x da folha que está em contato com o ar temos:

d q c = h - A p ,   t d x L ⋅ T x - T ∞

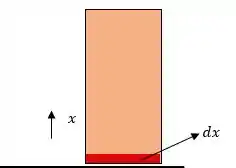
Por analogia a formula d q c = h - d x P T x - T ∞ , temos:

P e f = A p ,   t L = 0,12   m 2 0,04   m = 3,0   m

Da equação 3.25 com k s = k b

k e f = k f + 2 k b - 2 ε k b - k f k f + 2 k b - ε k b - k f ⋅ k b

Para k f = 0,0282   W m ⋅ K e k b = 58   W m ⋅ K

k e f = 34,7 W m ⋅ K

Passo 3

Temos que a eficiência da folha de um elemento d x é dada pela equação 11.4 , onde A c é a área transversal a folha, logo temos:

A c = W ⋅ t = 0,04   m ⋅ 0,01   m = 4 ⋅ 10 - 4   m 2

m L f = h - ⋅ P e f k e f ⋅ A c ⋅ L 2  

Para os dados encontrados:

m L f = 18,7

Agora sim a eficiência da equação 11.4 é dada por:

η f = t g h   m L f m L f = t g h   18,7 18,7 = 0,0535

Lembrando que t g h é a tangente hiperbólica!

t g h   t = e t - e - t e t + e - t

Estamos quase lá! Agora vamos calcular a resistência térmica da folha em análise temos:

R t ,   f = 1 h - ⋅ A p ,   t ⋅ η f

R t ,   f = 0,0384   K W

Passo 4

Agora finalmente podemos avançar pro final dessa questão, estão preparados?! Pois vamos lá!

A capacitância calorifica da nossa esponja é dada por:

C m i n =   m ˙ c ⋅ c c ,   p = ρ V A c ,   b c p = 1,0782   k g m 3 ⋅ 10 m s ⋅ 1008   J k g ⋅ K

C m i n = 17,4   W K

Calculando a eficiência térmica do trocador de calor é:

ε = 1 - e - N T U

N T U = 1 R t ,   f ⋅ C m i n

Assim:

ε = 0,776

FINALMENTE PODEMOS CALCULAR NOSSA TAXA DE CALOR!!!

A taxa de calor é dada por:

q = ε ⋅ C m i n T s - T i

q = 0,776 ⋅ 17,4   W K ⋅ 80 ° C - 20 ° C

q = 810   W

É um resultado próximo do valor real, entretanto o gradiente de fluxo que atravessa a esponja não é levado em conta, assim o valor real da troca de calor será menor do que o encontrado!

Isso é tudo pessoal! \o/

Resposta

q = 810   W

É um resultado próximo do valor real, entretanto o gradiente de fluxo que atravessa a esponja não é levado em conta, assim o valor real da troca de calor será menor do que o encontrado!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

42 - Vapor de água saturado a 110℃ ℃ é condensado em um trocador de calor casco e tubos (1 passe no casco; 2, 4, … passes nos tubos) com um valor de U A de 2,5k W / K . A água de resfriamento entra a
38 - Por questões de saúde, espaços públicos requerem a substituição contínua de uma certa massa de ar interno viciado por ar externo fresco. Para conservar energia durante a estação de aquecimento, é
47 - Considere um trocador de calor bitubular muito comprido com temperaturas de entrada da água quente e da água fria de 85 e 15 ℃ ℃. A vazão da água quente é duas vezes a da água fria. Considerando
41 – Um aquecedor de água de alimentação, que abastece uma caldeira, é constituído por um trocador de calor casco e tubos com um passe no casco e dois passes nos tubos. Ele tem cem tubos com paredes d
43 - Um trocador de calor casco e tubos (1 passe no casco, 2 passes nos tubos) deve ser usado para condensar 2,73k g / s de vapor de água saturado a 340K . A condensação ocorre na superfície externa d