Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 31

Em determinado instante do tempo, a distribuição de temperaturas em uma parede com 0,3   m   de espessura é   T ( x )   =   a   +   b x   +   c x 2   , em que T   está em graus Celsius e x   em metros, a   =   – 200 ° C ,   b   =   – 200 ° C / m   e   c   =   30 ° C / m 2 . A parede tem uma condutividade térmica igual a 1   W / ( m   ·   K ) .  

  1. Com base em uma superfície de área unitária, determine a taxa de transferência de calor para dentro e para fora da parede, bem como a taxa de variação da energia acumulada no interior da parede.

  2. Se a superfície fria estiver exposta a um fluido a   100 ° C , qual é o coeficiente de transferência de calor por convecção?

Passo 1

Bora para mais uma questão \o/. Nessa questão nós temos a espessura de uma parede, sua condutividade térmica, distribuição de temperatura e temperatura do fluido. Para entender melhor fiz essa imagem para você

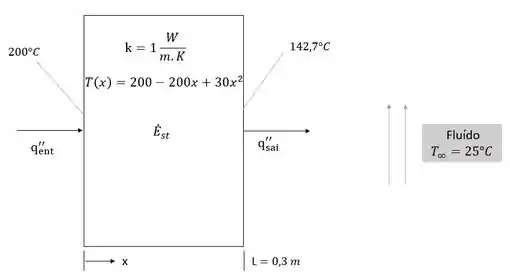
Aqui, nós queremos encontrar as taxas de calor da superfície, a taxa de variação de energia acumulada da parede por unidade de área e o coeficiente de convecção.

Passo 2

Para resolver essa questão vamos assumir que a condução é unidimensional em x e que k é constante.

Na letra (a) queremos saber a taxa de transferência de calor para dentro e para fora da parede e a taxa de variação da energia acumulada no interior da parede. Então, precisamos utilizar a Lei de Fourier:

q x ' ' = - k ∂ T ∂ x = 200 - 60 x . k

q e n t ' ' = q x = 0 ' ' = 200 ° C m × 1 W m . K = 200 W / m 2

q s a i ' ' = q x = L ' ' = 200 - 60 × 0,3 ° C m   × 1 W m . K = 182   W / m 2  

Fazendo um balanço de energia considerando a parede como volume de controle, temos:

E ˙ e n t ' ' - E ˙ s a i ' ' = E ˙ s t ' '

E ˙ s t ' ' = q e n t ' ' - q s a i ' ' = 18   W / m 2

Passo 3

Já na letra (b), queremos o coeficiente de transferência de calor por convecção. Então vamos aplicar um balanço de energia na superfície quando x = L , e vamos obter:

q s a i ' ' = h [ T L - T ∞ ]

h = q s a i ' ' T L - T ∞ = 182 W m 2 142,7 - 100 ° C

h = 4,3 W m 2 . K

Resposta

(a)   q e n t ' ' = 200 W / m 2 , q s a i ' ' = 182   W / m 2   e     E ˙ s t ' ' = 18   W / m 2

(b)   h = 4,3 W m 2 . K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema unidimensional, mostrado na figura, tem massa M , propriedades constantes, não apresenta geração de calor em seu interior e encontra-se inicialmente a uma temperatura uniforme T i . O aquece
Uma parede plana composta e unidimensional tem espessura global igual a 2 L . O Material A está no domínio - L≤x≤0 e há no seu interior uma reação química exotérmica que ocasiona uma taxa de geração v
Um dispositivo eletrônico em forma de disco, com espessura L d , diâmetro D e condutividade térmica k d , dissipa potência elétrica a uma taxa constante P e em uma de suassuperfícies. O dispositivo é
Um arranjo experimental para medir a condutividade térmica de materiais sólidos envolve o uso de dois bastões longos, equivalentes em todos os aspectos, exceto que um é fabricado com um material padrã
Água é aquecida em um tanque com tubos submersos de cobre, com paredes delgadas e diâmetro de 50 mm, nos quais escoam gases de combustão (T,.= 750 K). Para melhorar a transferência de calor para a águ