Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 68

Tipicamente, ar é aquecido em um secador de cabelos ao ser soprado através de um fio enrolado, no qual passa uma corrente elétrica. Energia térmica é gerada pelo aquecimento resistivo elétrico no interior do fio e é transferida por convecção da superfície do fio para o ar. Considere condições nas quais o fio está inicialmente a temperatura do ambiente, T i , e o aquecimento resistivo é iniciado em conjunto com o escoamento do ar em t   =   0 .

(a) Para um raio de fio r 0 , uma temperatura do ar T ∞ e um coeficiente convectivo h , escreva a forma da equação do calor e as condições inicial e de contorno que descrevem a resposta térmica transiente, T ( r ,   t ) , do fio.

(b) Para um comprimento e um raio do fio de 500   m m e 1   m m , respectivamente, qual é a taxa volumétrica de geração de energia térmica correspondente a um consumo de potência de P e l e =   500   W ? Qual é o fluxo térmico convectivo em condições de regime estacionário?

(c) Em coordenadas T   -   r , esboce as distribuições de temperaturas para as seguintes condições: condição inicial   ( t   ≤   0 ) , condição de regime estacionário ( t   →   ∞ ) , e dois tempos intermediários.

(d) Em coordenadas q r ' ' -   t , esboce a variação do fluxo térmico com o tempo nas posições r   =   0 e r   =   r 0 .

Passo 1

Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional com geração de energia, logo a troca de calor só ocorre em uma direção que no caso apresentado é a radial, vamos fazer nosso diagrama pra facilitar nossa vida.

Origem e sentido da geração de calor e da dissipação.

Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - C o n d u ç ã o   u n i d i m e n s i o n a l

I I - P r o p r i e d a d e s   c o n s t a n t e s

I I I - g e r a ç ã o   d e   c a l o r   v o l u m é t r i c a   c o n s t a n t e

I V -   E f e i t o   d e   r a d i a ç ã o   d e s p r e z i v e l   n a   s u p e r f i c i e   d o   f i o

Passo 2

(a)

Tendo tudo isso em mente vamos a nossa letra (a), o gráfico de T ( x ,   t ) em função do espaço. Para isso vamos escrever nossa lei de Fourier para coordenadas cilíndricas que fica assim:

Como nossa condução é unidimensional e há geração de energia, temos:

1 r r ∂ T ∂ r + q ˙ k = 1 α ∂ T ∂ t

Nossa condição inicial é:

T r ,   0 = T i

Aplicando nossas condições de contorno, temos:

r = 0 ,   ∂ T ∂ r = 0

r = r 0 , - k ∂ T ∂ r = h T r 0 ,   t - T ∞  

Passo 3

(b) A geração de energia volumétrica é dada por:

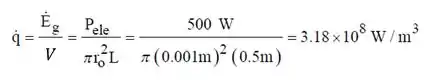
No estado permanente pelo balanço de energia temos que E ˙ g - E ˙ s a i = 0 nossa geração de energia volumétrica fica.

Passo 4

(c) Seguindo as equações da letra (a) vamos montar nosso gráfico T - r assim temos.

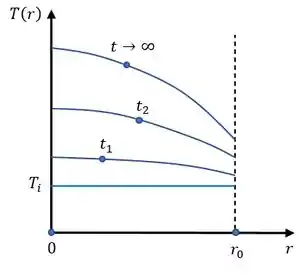
Passo 5

(d) Seguindo as equações da letra (a) vamos montar nosso gráfico q r ' ' - t

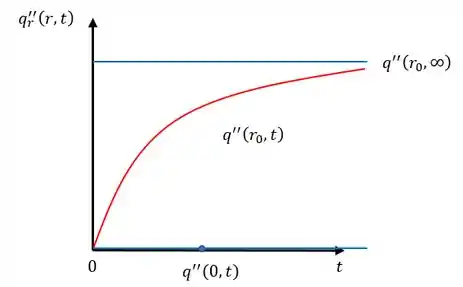
Isso é tudo pessoal! \o/

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Vapor d’água superaquecido a 575 ° C é conduzido de uma caldeira para a turbina de uma usina de geração de potência elétrica através de tubos de aço ( k = 35W / ( m · K ) ), com diâmetro interno igual
Uma parede composta cilíndrica é constituída por dois materiais com condutividades térmicas k A e k B , que estão separados por um aquecedor elétrico resistivo muito fino. As resistências de contato n
Uma corrente elétrica de 700A passa em um cabo de aço inoxidável com diâmetro de 5m m e resistência elétrica de 6 x 10 - 4Ω / m (ou seja, por metro de comprimento do cabo). O cabo encontra-se em um am
Seja o sistema de armazenamento de oxigênio líquido e as condições ambientes do laboratório descritas no Problema 1.49. Para reduzir a perda de oxigênio por evaporação, uma camada de isolante deve ser
Um tanque de armazenamento possui uma seção cilíndrica, com comprimento e diâmetro interno de L = 2m e D i = 1m , respectivamente, e duas calotas hemisféricas nas extremidades. O tanque é fabricado em