Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 08
Uma análise termodinâmica de uma turbina a gás com ciclo Brayton fornece como produção de potência líquida. O compressor, a uma temperatura média de , é impulsionado pela turbina a uma temperatura média de , por intermédio de um eixo com de comprimento e de diâmetro, com condutividade térmica .
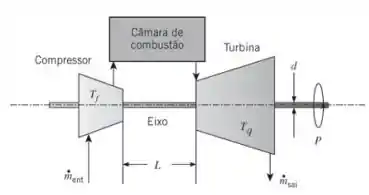
- Compare a taxa por condução em regime estacionário através do eixo que conecta a turbina quente ao compressor aquecido com a potência líquida prevista pela análise baseada na termodinâmica.
- Uma equipe de pesquisa propõe uma redução de escala da turbina a gás da parte (a), mantendo todas as dimensões nas mesmas proporções. A equipe supõe que as mesmas temperaturas quente e fria do item (a) se mantêm e que a potência líquida produzida pela turbina a gás é proporcional ao volume global do modelo. Represente graficamente a razão entre a condução através do eixo e a potência líquida produzida pela turbina na faixa . O modelo em escala reduzida com é factível?
Passo 1
Fala aí! Vamos resolver esse carinha aí? Partiu!
Bem, Temos duas letrinhas para resolver… Mas antes vamos começar anotando todos os nossos dados pra gente não se perder, beleza?
Agora sim vamos começar a resolver!
Passo 2
Começando pela letra a, precisamos calcular a taxa de transferência de calor, para comparar ela com a potência… Vamos lá então!
Opa! Precisamos da área e do fluxo térmico! Podemos achar eles, assim olha só:
Vamos substituir cada um, para resolver uma equação só, beleza?
Show! Agora vamos comparar fazendo a razão entre a taxa de transferência de calor e a potência líquida, beleza?
Show de bola! Vimos a relação entre as duas, agora vamos partir pra letra b.
Passo 3
Opa! Essa letra b, parece complexa, mas relaxa que não vai dar conta junto!
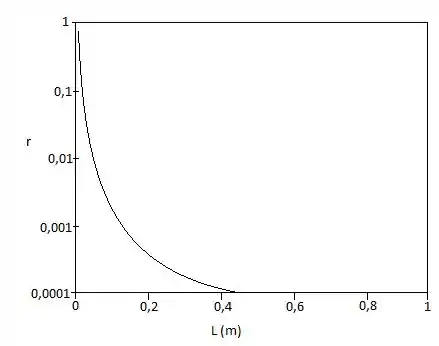
O enunciado que que a gente faça um gráfico da razão entre a condução através do eixo e a potência líquida produzida pela turbina, na faixa que ele nos deu…
Bom, antes de tudo ele fala pra gente que as dimensões terão uma escala reduzida e que a potência líquida é proporcional ao volume…
O que ele está querendo dizer é o seguinte: nosso diâmetro e potência serão reduzidos proporcionalmente com relação a um volume!
Então nós tínhamos um:
Que serão reduzidos, assim olha só:
Não se assusta, esse aí ficará em função, pra gente montar o gráfico na faixa que foi dada, belezinha?
Agora vamos refazer a razão entre a transferência de calor e potência, show?
Vamos fazer do mesmo jeitinho, ok?
Só que agora o nosso e o nosso são diferentes… Vamos substituí-los ali:
Passo 4
Agora vamos substituir nosso dados, mas vamos manter em função do , show?
Show! Conseguimos a razão, agora vamos fazer o teste para saber se é possível nosso :
Olha só, a nossa relação entre a transferência de calor e a potência líquida deu , mas temos que ver que o conceito de turbina muito pequena não é algo viável, beleza?
Então vemos que o modelo reduzido não é factível, certo?
Agora vamos exibir graficamente o comportamento da razão entre transferência de calor e da potência e o nosso :
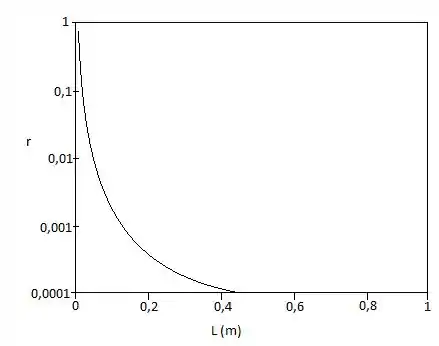
Conseguimos! Acabamos com a questão!
Resposta
- ; O modelo reduzido não é factível.
