Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 8

Uma pequena fonte de radiação A 1 emite difusamente com uma intensidade I 1 =   1,2   ×   10 5   W / ( m 2 · s r ) . O detector de radiação A 2 está alinhado normal à fonte a uma distância L o   =   0,2   m . Uma tela opaca está posicionada na metade do caminho entre A 1 e A 2   para impedir que a radiação da fonte atinja o detector. A pequena superfície A m é um espelho difuso perfeito que permite que a radiação emitida pela fonte seja refletida para o detector.

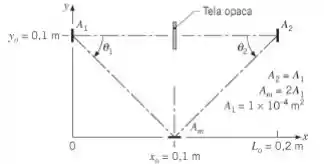
(a) Calcule a potência radiante incidente em A m devido à emissão a partir da fonte A 1 ,   q 1 → m ( W ) .

(b) Supondo que a potência radiante, q 1 → m , seja refletida perfeita e difusamente, calcule a intensidade deixando A m ,   I m ( W / ( m 2 · s r ) ) .  

(c) Calcule a potência radiante incidente em A 2 devido à radiação refletida deixando A m ,   q m → 2   ( μ W ) .  

(d) Represente graficamente a potência radiante q m → 2 como uma função da distância de separação lateral y o na faixa 0   ≤   y o   ≤   0,2   m . Explique as características da curva resultante

Passo 1

Nessa questãozitcha nós temos que a radiação de uma fonte radiante difusa A 1 com intensidade I 1   =   1,2   ×   10 5   W / m 2 . s r é incidente no espelho A m , que reflete a radiação no detector de radiação A 2 .

Com isso, queremos encontrar a intensidade de potência radiante em A m devido a emissão da fonte, A 1 ,   a intensidade da potência radiante que sai do espelho difuso e perfeitamente refletido e a potência radiante incidente no detector A 2 devido à radiação refletida que deixa A m .

Passo 2

Vamos lá! Para resolver a questão vamos assumir:

(1) A superfície A 1 emite difusivamente;

(2) A superfície A m não emite, mas reflete perfeita e difusamente;

(3) As áreas de superfície são muito menores que o quadrado de suas distâncias de separação;

A potência radiante que sai de A 1 incidente em A m é:

q 1 → m = I 1 A 1 cos ⁡ θ 1 Δ ω m - 1

Onde ω m - 1 é o ângulo sólido A m em relação a A 1 ,

Δ ω m - 1 ≡ d A n r 2 = A m cos ⁡ θ m   x o 2 y o 2 = 2 × 10 - 4 m 2 . cos ⁡ 45 ° 0,1 2 + 0,1 2   m 2 = 7,07 × 10 - 3 s r

Com, θ m = 90 ° - θ 1 e θ 1 = 45 ° ,

q 1 → m = 1,2   ×   10 5 W m 2 · s r × 1 × 10 - 4 m 2 × cos ⁡ 45 ° × 7,07 × 10 - 3 s r = 60   m W  

Passo 3

A intensidade da radiação que sai de A m , após uma reflexão perfeita e difusa, é:

I m = q 1 → m A m π = 60 × 10 - 3 W π × 2 × 10 - 4 m 2 = 955 W m 2 . s r

A potência radiante que sai de A m devido à radiação refletida é,

q m → 2 = q 2 = I m A m cos ⁡ θ m Δ ω 2 - m

Onde Δ ω 2 - m é o ângulo sólido que A 2 subtende em relação a A m ,

Δ ω 2 - m ≡ d A n r 2 = A 2 cos ⁡ θ 2   L o - x o 2 + y o 2 = 1 × 10 - 4 m 2 . cos ⁡ 45 ° 0,1 2 + 0,1 2   m 2 = 3,54 × 10 - 3 s r

Com θ 2 = 90 ° - θ m ,

q m → 2 = q 2 = 95,5 W m 2 · s r × 2 × 10 - 4 m 2 × cos ⁡ 45 ° × 3,54 × 10 - 3 s r = 47,8   μ W  

Resposta

  1. q 1 → m = 60   m W  
  2. I m = 955 W m 2 . s r
  3. q m → 2 = 47,8   μ W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Admitindo que a superfície da Terra seja negra, estime sua temperatura considerando que o Sol tenha uma temperatura equivalente a de um corpo negro a 5800 K. Os diâmetros do Sol e da Terra são de 1,39
Um elemento aquecedor radiante em forma de um anel é energizado eletricamente e mantido a uma temperatura Ta = 3000 K. O elemento aquecedor é usado em um processo de fabricação para aquecer uma pequen
Fornos isotérmicos com pequenas aberturas, que se aproximam de um corpo negro, são usados com frequência para calibrar medidores de fluxo térmico, termômetros de radiação e outros equipamentos radiomé
Considere uma pequena superfície com área A 1=10 – 4 m 2 , que emite difusamente com um poder emissivo hemisférico total de E 1=5×10 4W / m 2 . (a) A que taxa essa emissão é interceptada por uma peque
Qual é a irradiação nas superfícies A 2 ,A 3 e A 4 do Exemplo 12.1 devido à emissão a partir de A 1 ?