Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 59

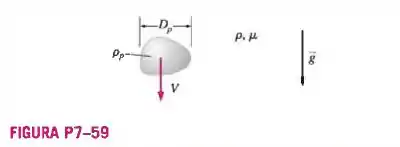
Uma pequena partícula de aerossol de densidade ρ p e diâmetro característico D p cai no ar de densidade ρ e viscosidade μ (Figura P7-59). Se a partícula for suficientemente pequena, a

aproximação do escoamento lento é válida, e a velocidade terminalda partícula V depende apenas de μ , da constante gravitacional g e da diferença de densidade ( ρ p - ρ ) . Use a análise

dimensional para gerar uma relação para V como função das variáveis independentes. Cite todos os parâmetros adimensionais usuais que aparecem em sua análise.

Passo 1

Bora lá!! Vamos dar aquela olhadinha no enunciado pra poder listar os parâmetros relevantes!!

V = f D p , ρ p - ρ , μ ,   g

Temos então 5   parâmetros relevantes!!

n = 5

Passo 2

Agora a gente precisa listar as dimensões primárias de cada parâmetro!

V = L 1 t - 1

D p = L 1

ρ = m 1 L - 3

μ = m - 1 L - 1 t - 1

g = { m 1 t - 2 }

Passo 3

Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões m ,   L e t , então podemos considerar:

j = 3

Teorema de Pi de Buckingham:

k = n - j

O n a gente já tinha achado no Passo 1, lá vimos que n = 5 !

Substituindo:

k = 5 - 3 = 2

Nesse caso o número de grupos π esperado é igual a 2. Então vamos atrás deles!!

Passo 4

Antes de começar a precisamos decidir quais vão ser os 3   parâmetros repetidos.

Como V é o parâmetro dependente, não podemos escolher ele!

Eu vou escolher D p , ρ p - ρ   e     g por serem parâmetros mais simples!

Passo 5

Agora sim, vamos encontrar o nosso primeiro grupo π !!

Começando com o π 1 que vai ser o π dependente!!

Organizando os nossos parâmetros a gente fica com:

π 1 = 1 = { ( V ) × D p a × ρ p - ρ b × g c }

Escrevendo suas dimensões básicas:

π 1 = m 0 L 0 t 0 = { ( L 1 t - 1 ) × L 1   a × m 1 L - 3 b × L 1 t - 2 c }

Agora equacionando:

Massa:

m 0 = m b

b = 0

Comprimento:

L 0 = L 1 × L a × L - 3 b × L c

0 = 1 + a - 3 b + c

0 = 1 + a - 0 + c

Tempo:

t 0 = t - 1 × t - 2 c

0 = - 1 - 2 c

c = - 1 2

Logo:

0 = 1 + a - 0 + c

0 = 1 + a - 1 2

a = - 1 2

Substituindo a , b e c , temos:

π 1 = { ( V ) × D p - 1 2 × ρ p - ρ 0 × g - 1 2 }

Organizando:

π 1 = V D p g

Esse é o número de Froude!  

Agora vamos achar π 2 , esse vai ser nosso π independente combinando as nossas variáveis repetidas com μ :

π 2 = 1 = { ( μ ) × D p d × ρ p - ρ e g f }

Escrevendo suas dimensões básicas:

π 2 = m 0 L 0 t 0 = { ( m 1 L - 1 t - 1 ) × L 1   d × m 1 L - 3 e × L 1 t - 2 f }

Agora equacionando:

Massa:

m 0 = m 1 × m e

0 = 1 + e

e = - 1

Comprimento:

L 0 = L - 1 × L d × L - 3 e × L f

0 = - 1 + d - 3 e + f

0 = - 1 + d + 3 + f

Tempo:

t 0 = t - 1 × t - 2 f

0 = - 1 - 2 f

f = - 1 2

Logo:

0 = - 1 + d + 3 + f

0 = - 1 + d + 3 - 1 2

d = 2 2 - 6 2 + 1 2 = - 3 2

Substituindo:

π 2 = 1 = { ( μ ) × D p - 3 / 2 × ρ p - ρ - 1 g - 1 / 2 }

π 2 = μ ρ p - ρ √ D p   3 g

Se a gente da uma organizadinha e inverte o numerador com o denominador, ficamos com:

π 2 = ρ p - ρ D p D p   g μ = R e

Onde D p   2 g é a velocidade.

Passo 6

Agora vamos escrever a relação entre os dois grupos π :

V D p g = f ρ p - ρ D p D p   g μ

Resposta

V D p g = f ρ p - ρ D p D p   g μ

Os parâmetros relevantes utilizados formam: Velocidade ( V ) , diâmetro da particula, ( d p ) , densidade relativa ( ρ p - ρ ) e gravidade ( g ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A emissão de vórtices pode ser usada para projetar um medidor de vazão tipo vórtice (Figura 6.33). Uma barra rombuda montada transversalmente no tubo emite vórtices cuja frequência é medida por um sen
Se a viscosidade for desprezada, os resultados típicos do escoamento na bomba do Exemplo 5.3 são mostrados na Figura P5.61 para um modelo de bomba testado na água. O aumento de pressão diminui e a pot
No Problema P5.61 seria difícil resolver em função de ômega porque ele aparece nos três coeficientes adimensionais da bomba. Considere que, no Problema 5.61, omega seja desconhecido mas D = 12 cm e Q
Modifique o Problema P5.61 da seguinte forma: seja omega = 32 r/s e Q = 24 m3/h para uma bomba geometricamente semelhante. Qual é o diâmetro máximo se a potência não deve ultrapassar 300 W? Resolva es
Sabendo que Dp é proporcional a L, reformate os dados do Exemplo 5.10 para fazer o gráfico adimensional de Dp em função do diâmetro adimensional. Use esse gráfico para encontrar o diâmetro necessário