Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 87
No Problema P5.61 seria difícil resolver em função de ômega porque ele aparece nos três coeficientes adimensionais da bomba. Considere que, no Problema 5.61, omega seja desconhecido mas D = 12 cm e Q =25 m3/h. O fluido é gasolina a 20°C. Reformate os coeficientes, usando os dados do Problema P5.61, para fazer um gráfico da potência adimensional em função da rotação adimensional. Use esse gráfico para encontrar a máxima rotação omega para a qual a potência não ultrapassará 300 W.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, nós vamos tentar uma abordagem diferente para o Problema 5.61. Lá, a gente tinha um protótipo de uma bomba centrífuga, onde foram deduzidos dois grupos adimensionais, dados por:
Sendo: a potência da bomba; a massa específica do fluido; a rotação da bomba; o diâmetro do rotor da bomba e a vazão volumétrica do escoamento.
Além disso, o gráfico do Problema 5.61 nos fornece uma relação entre esses dois grupos adimensionais:
O enunciado desta questão pede que a gente encontre a rotação para uma potência , bombeando gasolina ().
Mas qual é nosso problema? Se a gente fizesse um gráfico de em função de ficaria muito difícil resolver pra encontrar , pois o termo está no denominador dos dois grupos adimensionais com potências diferentes.
A questão propõe então que a gente faça uma reformatação do problema e construa um gráfico de um novo termo de potência adimensional e encontre o valor de para essa situação.
Então vem comigo pra gente resolver esse problema juntos!
Passo 2
Em primeiro lugar, vamos encontrar um novo grupo adimensional que não dependa da rotação e dependa diretamente de e .
Vamos analisar novamente :
Para eliminar deveríamos multiplicar ambos os lados da equação por . Mas se quisermos manter a equação adimensional, devemos na verdade multiplicar por , pois assim as dimensões se cancelam.
Dessa forma, será dado por:
Mas se você prestar atenção vai ver que o grupo na verdade é nada mais que . Sendo assim:
Passo 3
Com a expressão obtida no passo anterior e com a relação entre e demonstrada no Passo 1, podemos simplesmente construir um gráfico de em função de , como demonstrado abaixo:
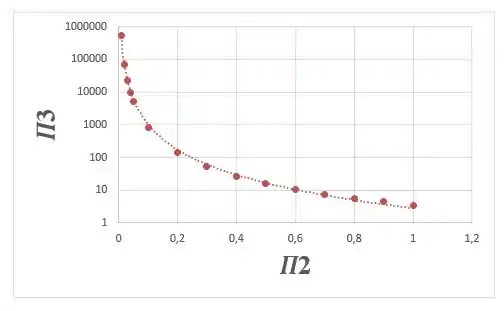
Para essa curva, um ajuste polinomial foi realizado, resultando na equação .
Agora, vamos calcular o valor de para as especificações do enunciado:
Substituindo em nosso ajuste polinomial, encontramos um valor de .
Com esse resultado, podemos finalmente calcular e finalizar o problema:
Pronto, matamos a questão juntos!
Resposta
A máxima rotação para a qual a potência não ultrapassará é