Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 89
Sabendo que Dp é proporcional a L, reformate os dados do Exemplo 5.10 para fazer o gráfico adimensional de Dp em função do diâmetro adimensional. Use esse gráfico para encontrar o diâmetro necessário na primeira linha de dados no Exemplo 5.10 se a queda de pressão for aumentada para 10 kPa para a mesma vazão, comprimento e fluido.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, nós vamos tentar uma abordagem diferente para o Exemplo 5.10.
Lá, foi deduzida uma expressão para a queda de pressão em função da velocidade média do escoamento (), viscosidade (), comprimento () e diâmetro () do tubo, dada por:
O enunciado nos pede para calcular o diâmetro do tubo a partir desta equação. O problema é que a velocidade é desconhecida, então iremos deduzir um novo grupo adimensional , independente da velocidade.
Depois, iremos plotar um gráfico de em função de outro grupo adimensional que devemos deduzir.
Por fim, com essa nova expressão, iremos calcular o diâmetro do tubo para os dados da primeira linha da tabela que ilustra o Exemplo 5.10, considerando uma queda de pressão .
Então vem comigo pra gente resolver esse problema juntos!
Passo 2
Em primeiro lugar, vamos encontrar um novo grupo adimensional que não dependa da velocidade .
Vamos analisar novamente pra equação que eu te mostrei no Passo 1:
Como primeiro passo, devemos substituir a velocidade por :
Para eliminar do lado esquerdo, devemos dividir ambos os lados da equação por . No entanto, para manter a equação adimensional, devemos multiplicar ambos os lados da equação por :
Podemos deduzir então, dois novos grupos adimensionais:
Logo, temos a seguinte relação:
Devemos então traçar o gráfico de em função de como pede a questão:
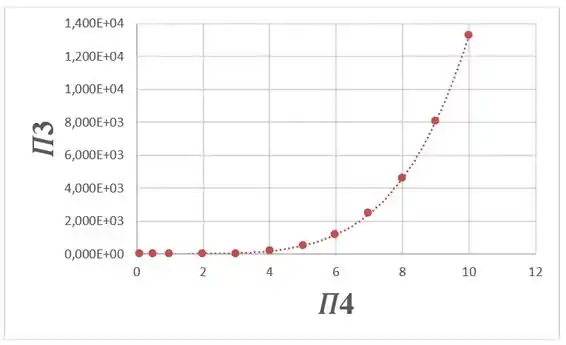
Passo 3
Com a expressão obtida no passo anterior e com a relação entre e , e com os dados da primeira linha da tabela do Exemplo 5.10, ou seja, , , e , podemos calcular o diâmetro.
Em primeiro lugar, vamos calcular :
Dessa maneira, temos que
E assim, finalmente podemos calcular :
Pronto, matamos a questão juntos!
Resposta
O diâmetro necessário é