Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 4
Um pequeno cubo de aço está suspenso na água por uma corda. Se os comprimentos das laterais do cubo forem muito pequenos, como você compararia as imensidades das pressões na parte superior, inferior e nas superfícies laterais do cubo?
Passo 1
Para entender melhor o que ta rolando, bora desenhar um esqueminha!
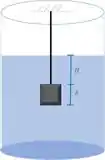
A questão quer que a gente analise cada face do nosso cubo! Então bora lá!
Passo 2
Supondo que o cubo tenha a aresta de comprimento , sendo que .
Vamos analisar primeiros as faces superior e inferior, considerando a pressão manométrica.
Primeiro a face superior:
Para a face inferior temos:
E para a face superior:
Agora para as laterais, como varia entre e , temos uma função linear:
Sendo um ponto qualquer da lateral da lateral do cubo.
Maaas, como já falamos anteriormente é uma dimensã muuuuuito pequenininha, praticamente zero, então podemos dizer que a pressão em todas as faces do cubo vão ser aproximadamente:
Resposta
As pressões em todos os lados do cubo são praticamente iguais.